Question

Negation of the Boolean statement (p ∨ q) ⇒ ((∼r) ∨ p) is equivalent to ______.

विकल्प

• p ∧ (∼q) ∧ r

• (∼p) ∧ (∼q) ∧ r

• (∼p) ∧ q ∧ r

• p ∧ q ∧ (∼r)

Answer 1

Negation of the Boolean statement (p ∨ q) ⇒ ((∼r) ∨ p) is equivalent to (∼p) ∧ q ∧ r.

Explanation:

The given statement is (p ∨ q)

⇒ (∼r ∨ p) ≡ ∼(P ∨ q) ∨ (∼r ∨ p)

Now, let us take the negation of an above statement

≡ ∼[∼(P ∨ q) ∨ (∼r ∨ P)]

≡ ∼[∼(P ∨ q) ∧ ∼(∼r ∨ P)]  ...{using De Margen’s law}

≡ (P ∨ q) ∧ (∼(∼r) ∧ ∼P) ...{∼(∼a) ≡ a}

≡ (P ∨ q) ∧ (r ∧ ∼P)

≡ [(P ∨ q) ∧ r] ∧ [(P ∨ q) ∧ (∼P)  ...{using distributive law}

≡ [(P ∨ q) ∧ r] ∧ [∼P]

Now let us draw its venn diagram

[(P ∨ q) ∼r]

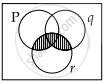
[(P ∨ q) ∼r] ∧ ∼P

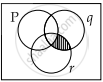
Now let us draw Venn diagram of each option:

p ∧ (∼q) ∧ r

(∼p) ∧ (∼q) ∧ r

∼p ∧ q ∧ r

p ∧ q ∧ (∼r)

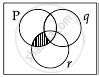
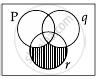
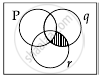
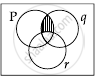
So, option (C) is correct.