Advertisements
Advertisements
प्रश्न
निम्नलिखित आकृति में दी हुई पतंग को बनाने के लिए प्रत्येक शेड (रंग) के कितने कागज की आवश्यकता होगी, यदि ABCD विकर्ण 44 cm वाला एक वर्ग है।
Advertisements
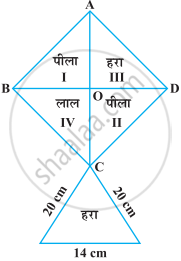
उत्तर
हम जानते हैं कि, वर्ग की सभी भुजाएँ सदैव बराबर होती हैं।
यानी, AB = BC = CD = DA
ΔACD में, AC = 44 cm, ∠D = 90°
ΔACD में पाइथागोरस प्रमेय का प्रयोग करने पर,
AC2 = AD2 + DC2
⇒ 442 = AD2 + AD2 ...[∵ DC = AD]
⇒ 2AD2 = 44 × 44
⇒ AD2 = 22 × 44
⇒ AD = `sqrt(22 xx 44)` ...[सकारात्मक वर्गमूल लेना क्योंकि लंबाई हमेशा धनात्मक होती है।]
⇒ AD = `sqrt(2 xx 11 xx 4 xx 11)`
⇒ AD = `22sqrt(2)` cm
तो, AB = BC = CD = DA = `22sqrt(2)` cm
∴ वर्ग ABCD का क्षेत्रफल = भुजा × भुजा
= `22sqrt(2) xx 22sqrt(2)`
= 968 cm2
∴ लाल भाग का क्षेत्रफल = `968/4` = 242 cm2 ...[चूँकि, वर्ग का क्षेत्रफल चार भागों में विभाजित है।]
अब, हरे भाग का क्षेत्रफल = `968/4` = 242 cm2
पीले भाग का क्षेत्रफल = `968/2` = 484 cm2
ΔPCQ में, भुजा PC = a = 20 cm, CQ = b = 20 cm और PQ = c = 14 cm
`s = (a + b + c)/2`
= `(20 + 20 + 14)/2`
= `54/2`
= 27 cm
∴ ΔPCQ का क्षेत्रफल = `sqrt(s(s - a)(s - b)(s - c))` ...[हीरोन के सूत्र द्वारा]
= `sqrt(27(27 - 20)(27 - 20)(27 - 14))`
= `sqrt(27 xx 7 xx 7 xx 13)`
= `sqrt(3 xx 3 xx 3 xx 7 xx 7 xx 13)`
= `21sqrt(39)`
= 21 × 6.24
= 131.04 cm2
∴ हरे भाग का कुल क्षेत्रफल = (242 + 131.04) = 373.04 cm2
अत:, एक पतंग बनाने के लिए प्रत्येक शेड के लिए आवश्यक कागज लाल कागज 242 cm2, पीला कागज 484 cm2 और हरा कागज 373.04 cm2 है।
APPEARS IN
संबंधित प्रश्न
एक यातायात संकेत बोर्ड पर 'आगे स्कूल है’ लिखा है और यह भुजा ‘a‘ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लंबाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
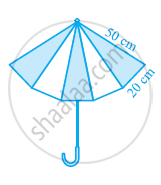
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों की सिलाई करके एक छाता बनाया गया है (देखिए आकृति) प्रत्येक टुकड़े के माप 20 सेमी, 50 सेमी और 50 सेमी हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
`2sqrt(3)` cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है
यदि एक समबाहु त्रिभुज का क्षेत्रफल `16sqrt(3)` cm2 है, तो इस त्रिभुज का परिमाप है
एक समांतर चतुर्भुज का आधार और संगत शीर्षलंब क्रमश : 10 cm और 3.5 cm हैं। उस समांतर चतुर्भुज का क्षेत्रफल 30 cm2 है।
एक त्रिभुजाकार मैदान जिसकी भुजाएँ 51 m, 37 m और 20 m हैं को 3 रु. प्रति m2 की दर से समतल कराने का व्यय 918 रु है।
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
एक समचतुर्भुज के आकार की शीट (चादर), जिसका परिमाप 40 cm और एक विकर्ण 12 cm है, को दोनों ओर से 5 रु प्रति m2 की दर से पेंट किया जाता है। पेंट करवाने की लागत ज्ञात कीजिए।
निम्नलिखित आकृति में, ∆ABC की भुजाओं में AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm है। आधार BC पर एक समांतर चतुर्भुज DBCE की रचना की जाती है, जो क्षेत्रफल में ∆ABC के बराबर है। इस समांतर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।
