Advertisements
Advertisements
प्रश्न
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
आकृति को देखिए। दर्शाइए AH > AB + BC + CD है।

उत्तर
प्रश्न में दिया गया है, AB, BC और CD रेखा के भाग हैं।
तब, AB + BC + CD = AD ...(i)
तथा AD रेखा AH का भाग है।
अब, यूक्लिड के अभिगृहीत 5 के अनुसार, संपूर्ण भाग से बड़ा है।
इसलिए, AH > AD
अर्थात लंबाई AH > AB + BC + CD की लंबाई का योग ...[(i) का प्रयोग करके]
APPEARS IN
संबंधित प्रश्न
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
नीचे दी हुई दो अभिधरणाओं पर विचार कीजिए:
- दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
- यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, C रेखाखंड AB का एक मध्य-बिंदु कहलाता है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है।
यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना
जाता है? (ध्यान दीजिए कि यह प्रश्न पाँचवीं अभिधरणा से संबंधित नहीं है।)
थेल्स निम्नलिखित देश का वासी था :
यदि एक राशि B एक अन्य राशि A का एक भाग है, तो A को B और एक अन्य राशि C के योग के रूप में लिखा जा सकता है।
वे कथन जिन्हें सिद्ध किया जाता है अभिगृहीत कहलाते है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, X और Y क्रमश : AC और BC के मध्य-बिंदु हैं तथा AX = CY है। दर्शाइए कि AC = BC है।
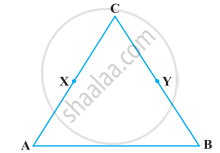
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।
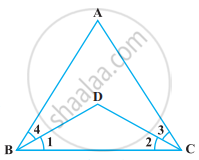
निम्नलिखित अभिगृहीतों को पढ़िए :
- वे वस्तुएँ जो एक ही वस्तु के बराबर हों, परस्पर बराबर होती हैं।
- यदि बराबर को बराबरों में जोड़ा जाए, तो पूर्ण बराबर होते हैं।
- वे वस्तुएँ जो एक ही वस्तु की दोगुनी हों, परस्पर बराबर होती है।
जाँच कीजिए कि क्या अभिगृहीतों का यह निकाय संगत है या असंगत है।
