Advertisements
Advertisements
प्रश्न

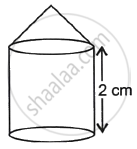
Observe the measures of pots In the given figure. How many jugs of water can the cylindrical pot hold?
उत्तर
The Radius of the conical water jug, r = 3.5 cm
Height of conical water jug, h = 10 cm
The radius of a cylindrical water pot, R = 7 cm
Height of cylindrical water pot, H = 10 cm
∴ The volume of the conical jug = \[\frac{1}{3} \mathrm\pi{r}^{2}\mathrm{h}\]
= \[\frac{1}{3}\times\pi\times3.5^{2}\times10\]
= \[\frac{1}{3}\times3.5^{2}\times10\pi \mathrm{cm}^{3}\]
∴ Volume of the cylindrical water pot = \[\pi\mathrm{R}^{2}\mathrm{H}\]
= \[\pi\times7^{2}\times10\]
=\[\mathrm{49}\times10\pi\mathrm{cm}^{3}\]
∴ Number of jugs = \[\frac{\mathrm{Volume~of~cylindrical~pot}}{\mathrm{Volume~of~conical~jug}}\]
= \[\frac{49\times10\pi}{\frac13\times3.5^{2}\times10\pi}\]
= \[\frac{49\times3}{3.5\times3.5}\]
= \[\frac{49\times3\times100}{35\times35}\]
= 12
∴ The cylindrical pot can hold 12 jugs of water.
संबंधित प्रश्न
Water flows at the rate of 15 m per minute through a cylindrical pipe, having the diameter 20 mm. How much time will it take to fill a conical vessel of base diameter 40 cm and depth 45 cm?
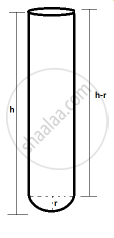
A test tube has diameter 20 mm and height is 15 cm. The lower portion is a hemisphere. Find the capacity of the test tube. (π = 3.14)
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m in diameter and 2 m deep. If the water flows through the pipe at the rate of 4 km per hour, in how much time will the tank be filled completely?
The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
A cylinder and a cone have equal bases. The height of the cylinder is 3 cm and the area of its base is 100 cm2. The cone is placed upon the cylinder. The volume of the solid figure so formed is 500 cm3. Find the total height of the figure.

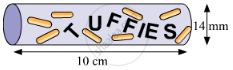
In the given figure, a cylindrical wrapper of flat tablets is shown. The radius of a tablet is 7 mm and its thickness is 5 mm. How many such tablets are wrapped in the wrapper?
A cylindrical bucket of diameter 28 cm and a height of 20 cm was full of sand. When the sand in the bucket was poured on the ground, the sand got converted into a shape of a cone. If the height of the cone was 14 cm, what was the base area of the cone?
A tin maker converts a cubical metallic box into 10 cylindrical tins. The side of the cube is 50 cm and the radius of the cylinder is 7 cm. Find the height of each cylinder so made, if the wastage of 12% is incurred in the process `(pi = 22/7)`
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
A capsule is in the shape of a cylinder with two hemispheres stuck to its ends. If the length of the entire capsule is 12 mm and the diameter of the capsule is 3 mm, how much medicine it can hold?
A right circular cylinder just encloses a sphere of radius r units. Calculate the curved surface area of the cylinder
A right circular cylinder just encloses a sphere of radius r units. Calculate the ratio of the areas of the sphere and cylinder
Suppose we have block of 4 kilogram kept on a horizontal surface and we are applying a horizontal force of 10 newton. Let the coefficient of friction is 0.2. Find the force of friction. Assume that g = 10.
Find volume of solid generated by revolving parabola y2. = 4ax, cut of by latus rectum, about tangent at vertex.
A right circular cylinder which is open at the top and has a given surface area, will have the greatest volume if its height h and radius r are related by
A cylinder and a cone have equal bases. The height of the cylinder is 2 cm and the area of its base is 64 cm2. The cone is placed upon the cylinder volume of the solid figure so formed is 400 cm3. Find the total height of the figure.