Advertisements
Advertisements
प्रश्न
Obtain an expression for the electric field intensity at a point outside uniformly charged infinite plane sheet.
उत्तर
- Consider a uniformly charged infinite plane sheet with uniform surface charge density (charge per unit area) σ kept in a medium of permittivity ε(ε = ε0k).
- By Gauss’ theorem, the net flux through a closed surface Φ = `"q"/ε_0` (for air/vacuum k = 1) ….(1)
where q is the total charge inside the closed surface. - To find the electric field due to a charged infinite plane sheet at P at a distance r from sheet, imagine a Gaussian surface around P in the form of a cylinder having cross-sectional area A and length 2r with its axis perpendicular to the plane sheet. The plane sheet passes through the middle of the length of the cylinder such that the ends of the cylinder (called end caps P and P') are equidistant (at a distance r) from the plane sheet as shown in the figure below.
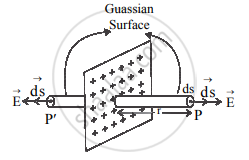
Charged infinite plane sheet - By symmetry electric field is perpendicular to the plane sheet and directed outwards, having the same magnitude at a given distance on either side of the sheet. The electric field is at right angles to the end caps and away from the plane. Its magnitude is the same at P and P'. The flux passing through the curved surface is zero as the electric field is tangential to this surface.
∴ The total flux through the closed surface is given by,
`phi = [oint"E""ds"]_"p" + [oint"E""ds"]_"p'"` ….(∵ θ = 0, cosθ = 1)
= EA + EA
∴ Φ = 2EA .........(2) - From equations (1) and (2),
`"q"/(ε_0)` = 2EA
∴ `(σ"A")/ε_0` = 2EA ............`(∵ σ = "q"/"A")`
∴ E = `σ/(2ε_0)`
This is the required expression.
APPEARS IN
संबंधित प्रश्न
Choose the correct option:
A parallel plate capacitor is charged and then isolated. The effect of increasing the plate separation on charge, potential, capacitance respectively are ______.
Answer in brief:
If the difference between the radii of the two spheres of a spherical capacitor is increased, state whether the capacitance will increase or decrease.
Answer in brief:
A spherical shell of radius b with charge Q is expanded to a radius a. Find the work done by the electrical forces in the process.
Choose the correct:
Charge + q and - q are placed at points A and B respectively which are distance 2L apart. C is the midpoint of A and B. The work done in moving a charge + Q from C to D, along the semicircle CD as shown in the figure below, is ______.
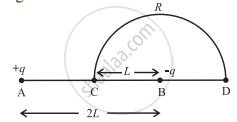
The work done in carrying a charge Q once round a circle of radius r with charge q at the centre of the circle is ______
The mean free path of electrons in a metal is 4 x 10-8m. Find the electric field, in units of V/m, which can give on an average 2 eV energy to an electron in the metal.
Obtain an expression for the capacitance of a parallel plate capacitor without a dielectric.
