Advertisements
Advertisements
प्रश्न
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
उत्तर
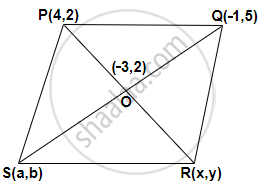
Let the coordinates of R and S be (x, y) and (a, b) respectively.
Mid-point of PR is O.
∴ `O(-3, 2) = O((4 + x)/2, (2 + y)/2)`
`-3 = (4 + x)/2, 2 = (2 + y)/2`
−6 = 4 + x, 4 = 2 + y
x = −10, y = 2
Hence, R = (−10, 2)
Similarly, the mid-point of SQ is O.
∴ `O(-3, 2) = O((a - 1)/2, (b + 5)/2)`
`-3 = (a - 1)/2, 2 = (b + 5)/2`
−6 = a – 1, 4 = b + 5
a = −5, b = –1
Hence, S = (−5, −1)
Thus, the coordinates of the point R and S are (−10, 2) and (−5, −1).
APPEARS IN
संबंधित प्रश्न
Find the mid-point of the line segment joining the points:
(5, –3) and (–1, 7)
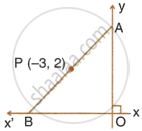
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
If (-3, 2), (1, -2) and (5, 6) are the midpoints of the sides of a triangle, find the coordinates of the vertices of the triangle.
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
If P(–b, 9a – 2) divides the line segment joining the points A(–3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC. P, Q and R are mid - points of sides BC, CA and AB respectively. Show that the centroid of ΔPQR is the same as the centroid ΔABC.
If (1, −2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the coordinates of D.
