Question

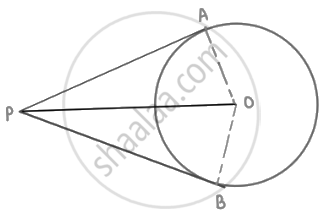
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______ 

  

विकल्प

• 55°

• 65°

• 85°

• 75°

Answer 1

PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = 55°.

Explanation:

   

∠OAP =∠OBP = 90°

∠AOP = 180°- 35° - 90°

∠AOP = 55°

OA = OB

AP = PB

OP is common base

Therefore ΔOAP ≅ ΔOBP

∠AOP = ∠BOP

∠BOP = 55°