Advertisements
Advertisements
प्रश्न
Point A (5, 1) on reflection on X- axis is mapped as A’. Also A on reflection on Y- axis is mapped as A”.
(i) Write the co-ordinates of A’.
(ii) Write the co-ordinates of A”.
(iii) Calculate the distance A’ A”.
(iv) On which coordinate axis does the middle point M of A” A’ lie?
उत्तर
(i) A' → (5, -1).
(ii) A'' → (-5, -1).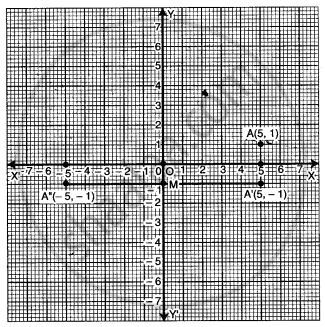
(iii) Distance A'A'' = 5 + 5 = 10.
(iv) Miles on Y-axis.
APPEARS IN
संबंधित प्रश्न
A point P is its own image under the reflection in a line l. Describe the position of point the P with respect to the line l.
A point P is reflected in the x-axis. Co-ordinates of its image are (–4, 5). Find the co-ordinates of P.
A point P is reflected in the x-axis. Co-ordinates of its image are (–4, 5). Find the co-ordinates of the image of P under reflection in the y-axis.
The point P(a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
The point A(–3, 2) is reflected in the x-axis to the point A’. Point A’ is then reflected in the origin to point A”.
- Write down the co-ordinates of A”.
- Write down a single transformation that maps A onto A”.
A triangle ABC lies in the co-ordinate plane. The co-ordinates of its vertices are A (2, 3), B ( 4,-4) and C (6 ,-7). This triangle is reflected in the line y=O onto LA'B'C'. LA'B'C' is then reflected in the origin ontolA"B"C". Write down the co-ordinates of LA'B'C' and LA "B" C".
Point A ( 4,-1) is reflected as A' in the line x= 1. Point B on reflection in the line y=3 is mapped as B' (6,-1). Write the co-ordinates of A' and B. Write the co-ordinates of mid.-ooint of the line sgment A' B'.
The image of a point P under reflection on the X-axis is (5, – 2). Write down the co-ordinates of P.
(i) Find the reflection of the point (3, 5) on X-axis.
(ii) Find the reflection of the point (- 3, 5) on X-axis.
(iii) Find the reflection of the point (- 3, – 5) on X-axis.
(iv) Find the reflection of the point (3, – 5) on X-axis.
P, Q have co-ordinates (-1, 2) and (6, 3) respectively. Reflect P on the X-axis to P’. Find:
(i) The co-ordinate of P’
(ii) Length of P’Q.
(iii) Length of PQ.
(iv) Is P’Q = PQ?
