Advertisements
Advertisements
प्रश्न
Prove the law of conservation of linear momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.
उत्तर
In nature, conservation laws play a very important role. The dynamics of motion of bodies can be analyzed very effectively using conservation laws. There are three conservation laws in mechanics. Conservation of total energy, conservation of total linear momentum, and conservation of angular momentum. By combining Newton’s second and third laws, we can derive the law of conservation of total linear momentum. When two particles interact with each other, they exert equal and opposite forces on each other.
Particle 1 exerts force `vecF_12` on particle 2 and particle 2 exerts an exactly equal and opposite force `vecF_12` on particle 1 according to Newton’s third law.
`vecF_12` = –`vecF_12` ……..(1)
In terms of momentum of particles, the force on each particle (Newton’s second law) can be written as –
`vecF_12 = (dvecp_1)/(dt)` and `vecF_12 = (dvecp_2)/(dt)` ……..(2)
Here `vecp_1` is the momentum of particle 1 which changes due to the force `vecF_12` exerted by particle 2. Further, Po is the momentum of particle `vecp_2` This changes due to `vecF_21` exerted by particle 1.
Substitute equation (2) in equation (1)
`(dvecp_1)/(dt) = -(dvecp_2)/(dt)` ...............(3)
`(dvecp_1)/(dt) + (dvecp_2)/(dt) = 0` ...............(4)
`d/dt(vecp_1 + vecp_2) = 0`
It implies that `vecp_1 + vecp_2` = constant vector (always).
`vecp_1 + vecp_2` is the total linear momentum of the two particles `(vecp_"tot" = vecp_1 + vecp_2)`. It is also called as total linear momentum of the system. Here, the two particles constitute the system. From this result, the law of conservation of linear momentum can be stated as follows.
If there are no external forces acting on the system, then the total linear momentum of the system (`vecp_"tot"`) is always a constant vector. In other words, the total linear momentum of the system is conserved in time. Here the word ‘conserve’ means that `vecp_1` and `vecp_2` can vary, in such a way that `vecp_1` + `vecp_2` is a constant vector.
The forces `vecF_12` and `vecF_21` are called the internal forces of the system because they act only between the two particles. There is no external force acting on the two particles from outside. In such a case the total linear momentum of the system is a constant vector or is conserved.
Meaning of law of conservation of momentum:
1. The Law of conservation of linear momentum is a vector law. It implies that both the magnitude and direction of total linear momentum are constant. In some cases, this total momentum can also be zero.
2. To analyze the motion of a particle, we can either use Newton’s second law or the law of conservation of linear momentum. Newton’s second law requires us to specify the forces involved in the process. This is difficult to specify in real situations. But conservation of linear momentum does not require any force involved in the process. It is convenient and hence important.
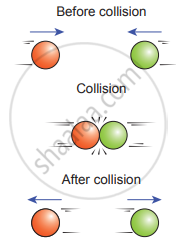
Collision of two particles
For example, when two particles collide, the forces exerted by these two particles on each other are difficult to specify. But it is easier to apply conservation of linear momentum during the collision process.
Examples:
Consider the firing of a gun. Here the system is Gun+bullet. Initially, the gun and bullet are at rest, hence the total linear momentum of the system is zero. Let `vecp_1` be the momentum of the bullet and `vecp_2` the momentum of the gun before firing. Since initially both are at rest,
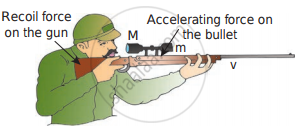
`vecp_1 = 0, vecp_2 = 0`.
Total momentum before firing the gun is zero, `vecp_1 + vecp_2` = 0. According to the law of conservation of linear momentum, total linear momentum has to be zero after the firing also.
When the gun is fired, a force is exerted by the gun in the bulletin forwarding direction. Now the momentum of the bullet changes from `vecp_1` to `vecp_1` To conserve the total linear momentum of the system, the momentum of the gun must also change from `vecp_2` to `vecp_2`. Due to the conservation of linear momentum, `vecp_1 + vecp_2^{'} = 0`.
It implies that `vecp_1^{'} = vecp_2^{'}`, the momentum of the gun is exactly equal, but in the opposite direction to the momentum of the bullet. This is the reason after firing, the gun suddenly moves backward with the momentum `(-vecp_2^{'})`. It is called ‘recoil momentum’. This is an example of the conservation of total linear momentum.
The outer edge of the road is slightly raised to avoid skidding
