Advertisements
Advertisements
प्रश्न
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
उत्तर
Given length of rectangular surface =6cm
Breath of rectangular surface = 4cm
Height (h) 1cm
Volume of a flat rec tan gular surface = lbh
= 6000 x 400 x 1
Volume = 240000cm3 .............(1)
Given radius of cylindrical vessel = 20cm
Let height off cylindrical vessel be h1
Since rains are transferred to cylindrical vessel.
So equating (1) with (2)
Volume of cylindrical vessel = `pir_1^2h_1`
`=22/7(20)^2xxh_1` .............(2)
24000`=22/7(20)^2xxh_1`
⇒h1 = 190.9cm
∴height of water in cylindrical vessel = 190 9cms
APPEARS IN
संबंधित प्रश्न
A heap of rice is in the form of a cone of base diameter 24 m and height 3.5 m. Find the volume of the rice. How much is canvas cloth required to just cover the heap?
How many balls each of radius 1cm can be made from a solid sphere of lead of radius
8cm?
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
A solid piece of iron of dimensions 49 × 33 × 24 cm is moulded into a sphere. The radius of the sphere is
A surahi is a combination of
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is needed?
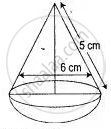
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Two solid cones A and B are placed in a cylinderical tube as shown in the figure. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder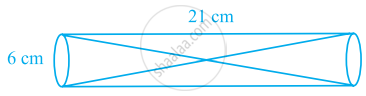
The largest sphere is carved out of a solid cube of side 21 cm. Find the volume of the sphere.
