Advertisements
Advertisements
प्रश्न
रेख AB, हा Y-अक्षाला समांतर असून A बिंदूचे निर्देशक (1, 3) आहेत तर, B बिंदूचे निर्देशक ______ असू शकतील.
विकल्प
(3, 1)
(5, 3)
(3, 0)
(1, -3)
उत्तर
रेख AB, हा Y-अक्षाला समांतर असून A बिंदूचे निर्देशक (1, 3) आहेत तर, B बिंदूचे निर्देशक (1, -3) असू शकतील.
स्पष्टीकरण:
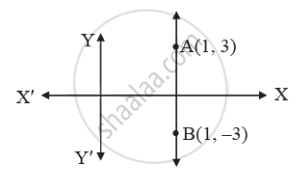
येथे, रेख AB || Y-अक्ष
∴ रेख AB वरील सर्व बिंदूंचे x-निर्देशक सारखेच असतील.
बिंदू A(1, 3) चा x निर्देशक = 1
बिंदू B(1, – 3) चा x निर्देशक = 1
∴ पर्याय (1, -3) अचूक आहे.
संबंधित प्रश्न
खाली दिलेल्या बिंदूंच्या प्रत्येक जोडीतील अंतर काढा.
P(-5, 7), Q(-1, 3)
खाली दिलेल्या बिंदूंच्या प्रत्येक जोडीतील अंतर काढा.
R(0, -3), S`(0, 5/2)`
खाली दिलेल्या बिंदूंच्या जोडीतील अंतर काढा.
L(5, -8), M(-7, -3)
खाली दिलेल्या बिंदूंच्या जोडीतील अंतर काढा.
W`((-7)/2 , 4)`, X(11, 4)
P(-2, 2), Q(2, 2) आणि R(2, 7) हे काटकोन त्रिकोणाचे शिरोबिंदू आहेत, हे पडताळून पाहा.
A(-4, -7), B(-1, 2), C(8, 5) आणि D(5, -4) हे ABCD या समभुज चौकोनाचे शिरोबिंदू आहेत हे दाखवा.
जर बिंदू L(x, 7) आणि बिंदू M(1, 15) यांना जोडणाऱ्या रेषाखंड LM ची लांबी 10 सेमी असेल, तर बिंदू x ची किंमत शोधा.
आरंभबिंदूचे निर्देशक लिहा.
बिंदू A(–1, 1) आणि बिंदू B(5, –7) आहेत, तर या दोन बिंदूंमधील अंतर काढा.
उकल:
समजा, A(x1, y1) आणि B(x2, y2)
x1 = –1, y1 = 1 आणि x2 = 5, y2 = – 7
अंतराच्या सूत्रानुसार,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
d(A, B) = `sqrt(square + [(-7) + square]^2)`
∴ d(A, B) = `sqrtsquare`
∴ d(A, B) = `square`
बिंदू A(–1, 1) आणि बिंदू B(5, –7) आहेत. तर या दोन बिंदूंना जोडणाऱ्या रेषाखंड AB च्या मध्यबिंदूचे निर्देशक लिहा.
उकल:
समजा, A(x1, y1) आणि B(x2, y2)
x1 = –1, y1 = 1 आणि x2 = 5, y2 = –7
मध्यबिंदूच्या सूत्रानुसार,
∴ रेषाखंड AB च्या मध्यबिंदूचे निर्देशक = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
∴ रेषाखंड AB च्या मध्यबिंदूचे निर्देशक = `(square/2, square/2)`
∴ रेषाखंड AB च्या मध्यबिंदूचे निर्देशक = `(4/2, square/2)`
∴ रेषाखंड AB च्या मध्यबिंदूचे निर्देशक = `(2, square)`
