Question

Sides AB and BC and median AD of a ΔABC are respectively proportional to sides PQ and PR and median PM of ΔPQR. Show that ΔABC ∼ ΔPQR.

Answer 1

Given that, AD and PM are medians of `triangle`ABC and `triangle`PQR, respectively.

Also,

`(AB)/(PQ) = (AC)/(PR) = (AD)/(PM)`

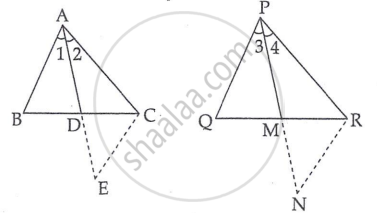
To prove: `triangle`ABC ∼ `triangle`PQR

Construction: Produce AD to E so that AD = DE and Join CE

Similarly, produce PM to N such that PM = MN, also Join RN.

Now, we have,

In `triangle`ABD and `triangle`CDE,

AD = DE       ...[By Construction]

BD = DC       ...[∵ AD is the median]

And, `angle`ADB = `angle`CDE        ...[Vertically opposite angles]

So, `triangle`ABD ≅ `triangle`CED        ...[By SAS Congruence criterion]

Also, AB = CE      ...[By CPCT]  ...(i)

In `triangle`PQM and ΔMNR,

PM = MN         ...[By Construction]

QM = MR        ...[∵ AD is the median]

And, `angle`PMQ = `angle`NMR        ...[Vertically opposite angles]

So, `triangle`PQM ≅ `triangle`MNR       ...[By SAS Congruence criterion]

Also, PQ = RN       ...[By CPCT]  ...(ii)

Now,

`(AB)/(PQ) = (AC)/(PR) = (AD)/(PM)`

From (i) and (ii),

`(CE)/(RN) = (AC)/(PR) = (AD)/(PM)`

`(CE)/(RN) = (AC)/(PR) = (2AD)/(2PM)`

`(CE)/(RN) = (AC)/(PR) = (AE)/(PN)`

So, `triangle`ACE ∼ `triangle`PRN       ...[By SSS similarity criterion]

Therefore, `angle`2 = `angle`4

Similarly, `angle`1 = `angle`3

Adding them,

`angle`1 + `angle`2 = `angle`3 + `angle`4

⇒ `angle`A = `angle`P        ...(iii)

Now, In `triangle`ABC and `triangle`PQR we have,

`(AB)/(PQ) = (AC)/(PR)`        ...[Given]

⇒ `angle`A = `angle`P        ...[from (iii)]

So, `triangle`ABC ∼ `triangle`PQR        ...[By SAS Similarity criteria]

Hence proved.