Question

समांतरभुज चौकोनाच्या चारही कोनांच्या दुभाजकांमुळे तयार झालेला चौकोन आयत असतो, हे सिद्ध करा.

Answer 1

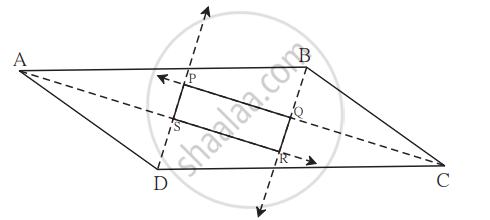
पक्ष: `square`ABCD हा समांतरभुज चौकोन आहे.

साध्य: `square`PQRS हा आयत आहे.

सिद्धता:

`square`ABCD हा समांतरभुज चौकोन आहे.     ...(पक्ष)

∠ADC + ∠BCD = 180°     ...(समांतरभुज चौकोनाचे लगतचे कोन पूरक असतात.)

दोन्ही बाजूंना `1/2` ने गुणून,

`1/2` ∠ADC + `1/2` ∠BCD = `1/2xx180°`      ...(i)

पण,

`1/2` ∠ADC = ∠PDC      ...(किरण DP हा ∠ADC चा दुभाजक आहे.)   ...(ii)

आणि `1/2` ∠BCD = ∠PCD     ...(किरण CP हा ∠BCD चा दुभाजक आहे.)   ...(iii)

∴ ∠PDC + ∠PCD = 90°      ...[(i), (ii) आणि (iii) वरून]   ...(iv)

ΔPDC मध्ये,

∠PDC + ∠PCD + ∠DPC = 180°    ...(त्रिकोणाच्या कोनांच्या मापांची बेरीज 180° असते.)

∴ 90° + ∠DPC = 180°       ...[(iv) वरून]

∴ ∠DPC = 180° – 90°

∴ ∠DPC = 90°

म्हणजेच ∠SPQ = 90°     ...(D-S-P, P-Q-C)   ...(v)

याचप्रमाणे, आपण सिद्ध करू शकतो, की ∠SRQ = 90°     ...(vi)

तसेच, ∠ASD = 90° आणि ∠BQC = 90°     ...(vii)

∠PSR = ∠ASD     ...(शिरोबिंदू कोन)

∴ ∠PSR = 90°     ...[(vii) वरून]    ...(viii)

तसेच, ∠PQR = 90°     ...(ix)

`square`PQRS मध्ये,

∠SPQ = ∠SRQ = ∠PSR = ∠PQR = 90°     ...[(v), (vi), (viii) आणि (ix) वरून]

∴ `square`PQRS हा आयत आहे.