Advertisements
Advertisements
प्रश्न
Solve by cross-multiplication method
6x + 7y – 11 = 0, 5x + 2y = 13
उत्तर
6x + 7y – 11 = 0 → (1)
5x + 2y = 13 → (2)
Use the coefficient for cross multiplication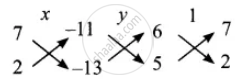
`x/(- 91 - (-22)) = y/(- 55 - (-78)) = 1/(12 - (35))`
`x/(- 91 + 22) = y/(-55 + 78) = 1/(12 - 35)`
`x/(-69) = y/23 = 1/(-23)`
But `x/(-69) = 1/(-23)`
– 23x = – 69
∴ 23x = 69
x = `69/23`
= 3
`y/23 = 1/(-23)`
– 23y = 23
23y = – 23
y = `- 23/23`
y = –1
∴ The value of x = 3 and y = –1
APPEARS IN
संबंधित प्रश्न
Solve, using cross-multiplication :
4x + 3y = 17
3x - 4y + 6 = 0
Solve, using cross-multiplication :
6x + 7y - 11 = 0
5x + 2y = 13
Solve, using cross-multiplication :
5x + 4y + 14 = 0
3x = -10 - 4y
Solve, using cross-multiplication :
4x - y = 5
5y - 4x = 7
Solve, using cross-multiplication :
4x - 3y = 0
2x + 3y = 18
Solve, using cross-multiplication :
4x - 3y - 11 = 0
6x + 7y - 5 = 0
Solve, using cross-multiplication :
4x + 6y = 15
3x - 4y = 7
Solve, using cross-multiplication :
0.4x - 1.5y = 6.5
0.3x + 0.2y = 0.9
Solve, using cross-multiplication :
√2x - √3y = 0
√5x + √2y = 0
Solve by cross-multiplication method
8x – 3y = 12, 5x = 2y + 7
