Advertisements
Advertisements
प्रश्न
Solve the following inequalities and graph their solution set:
`(2x - 5)/(x + 2) < 2`
उत्तर
The inequality `(2x - 5)/(x + 2) < 2` is
eqivalent to `(2x - 5)/(x + 2) - 2 < 0 ⇔ (2x - 5 - 2x - 4)/(x + 2) < 0`
⇒ `(-9)/(x + 2) < 0`
But `(a)/(b) < 0, a < 0`
⇒ b > 0
Thus, `(-9)/(x + 2) < 0, -9 < 0`
⇒ x > -2 > 0
⇒ x > -2
The graph of this solution is x > -2.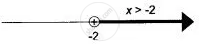
APPEARS IN
संबंधित प्रश्न
State, whether the following statements are true or false:
a < b, then a – c < b – c
If x ∈ N, find the solution set of inequations.
5x + 3 ≤ 2x + 18
If x ∈ N, find the solution set of inequations.
3x – 2 < 19 – 4x
If the replacement set is the set of real numbers, solve:
8 – 3x ≤ 20
Given x ∈ {whole numbers}, find the solution set of:
–1 ≤ 3 + 4x < 23
Solve and graph the solution set of:
x + 5 ≥ 4(x – 1) and 3 – 2x < –7, x ∈ R
Solve for x in the following in-equation, if the replacement set is R;
9 - 4x ≤ 15 - 7x
Find the solution set of the following inequalities and draw the graph of their solutions sets:
| 3 - 2x | ≥ 2
Find the solution set of the following inequalities and draw the graph of their solutions sets:
`|(x - 5)/(3)| < 6`
The maximum value of x for the inequation 4x ≤ 12 + x is ______.
