Advertisements
Advertisements
प्रश्न
State and prove Kirchoff’s law of heat radiation.
Prove Kirchhoff’s law of radiation theoretically.
उत्तर
Kirchhoff’s law of thermal radiation deals with wavelength specific radiative emission and absorption by a body in thermal equilibrium. It states that at a given temperature, the ratio of emissive power to coefficient of absorption of a body is equal to the emissive power of a perfect blackbody at the same temperature for all wavelengths.
Since we can describe the emissive power of an ordinary body in comparison to a perfect blackbody through its emissivity, Kirchhoff’s law can also be stated as follows: for a body emitting and absorbing thermal radiation in thermal equilibrium, the emissivity is equal to its absorptivity.
Symbolically, a = e or more specifically a(λ) = e(λ).
Thus, if a body has high emissive power, it also has high absorptive power and if a body has low emissive power, it also has low absorptive power.
Kirchhoff’s law can be theoretically proved by the following thought experiment. Consider an ordinary body A and a perfect blackbody B of identical geometric shapes placed in an enclosure. In thermal equilibrium, both bodies will be at same temperature as that of the enclosure.

Let R be the emissive power of body A, RB be the emissive power of blackbody B and a be the coefficient of absorption of body A. If Q is the quantity of radiant heat incident on each body in unit time and Qa is the quantity of radiant heat absorbed by the body A, then Qa = a Q. As the temperatures of the body A and blackbody B remain the same, both must emit the same amount as they absorb in unit time. Since emissive power is the quantity of heat radiated from unit area in unit time, we can write
Quantity of radiant heat absorbed by body A = Quantity of heat emitted by body A
or a Q = R ...(1)
For the perfect blackbody B,
Q = RB ...(2)
From Eqs. (1) and (2), we get,
a = `R/Q = R/R_b` ...(3)
From Eq. (3), we get, `R/a = R_b`
By definition of coefficient of emission,
`R/R_b` ...(4)
From Eqs. (3) and (4), we get, a = e.
Hence, the proof of Kirchhoff‘s law of radiation.
APPEARS IN
संबंधित प्रश्न
At temperature T, the emissive power and absorption power of a body for certain wavelength are `"e"_lambda` and `"a"_lambda` respectively, then ____________.
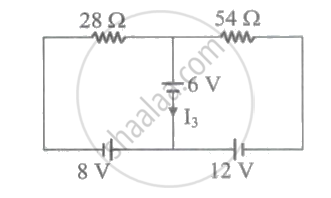
Consider the circuit shown in the figure. The current I3 is equal to ____________.
Half part of an ice block is covered with black cloth and rest half is covered with white cloth and then it is kept in sunlight. After some time, clothes are removed to see the melted ice. Which of the following statements is correct?
Kirchhoff's law of radiation proves that a good emitter is a ______.
