Advertisements
Advertisements
प्रश्न
State any two sources of errors in the meter-bridge experiment. Explain how they can be minimized.
उत्तर १
The chief sources of error in the meter bridge experiment are as follows:
- The cross-section of the bridge wire may not be uniform. The wire's resistance will not be proportional to its length since it will not have a consistent resistance per unit length.
- End resistances at the wire's two ends may be introduced as a result of
- the resistance of the metal strips
- the contact resistance of the bridge wire with the metal strips
- unmeasured lengths of the wire at the ends because the contact points of the wire with the metal strips do not coincide with the two ends of the metre scale attached.
Such errors are almost unavoidable but can be minimized considerably as follows:
- Readings must be taken by modifying the standard known resistance to obtain the null point close to the wire's centre. The null points should be in the middle one-third of the wire when taking multiple readings.
- The measurements must be repeated with the standard resistance (resistance box) and the unknown resistance swapped in the gaps of the bridge, and the averages of the two results obtained.
उत्तर २
Sources of errors:
- The cross-section of the wire may not be uniform.
- The ends of the wire are soldered to the metallic strip where contact resistance is developed, which is not taken into account.
- The measurements of lx and lR may not be accurate.
To minimize the errors
- The value of R is so adjusted that the null point is obtained around the middle one-third of the wire (between 34 cm and 66 cm) so that percentage error in the measurement of lx and lR is minimum and nearly the same.
- The experiment is repeated by interchanging the positions of unknown resistance X and known resistance box R.
- The jockey should be tapped on the wire and not slid. The jockey is used to detect whether there is a current through the central branch. This is possible only by tapping the jockey.
संबंधित प्रश्न
Explain with a neat circuit diagram how will you determine unknown resistance ‘X' by using meter bridge
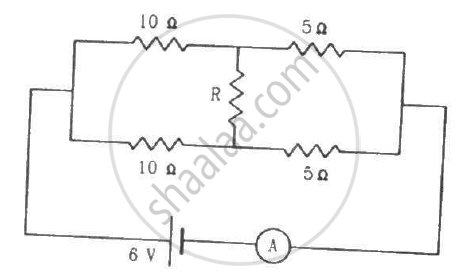
What should be the value of R in the figure for which the current in it is zero?
In Wheatstone’s meter-bridge experiment, the null point is obtained in the middle one-third portion of the wire. Why is it recommended?
Four resistances 4 Ω, 8Ω, XΩ and 12Ω are connected in a series to form Wheatstone’s network. If the network is balanced, the value of X is ______.
In conversion of moving coil galvanometer into an ammeter of required range, the resistance of ammeter, so formed is ______.
[S = shunt and G = resistance of galvanometer]
The current which flows in a galvanometer of Wheatstone bridge is directly proportional to ______
In a metre bridge experiment, the null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y. If X < Y, then where will be the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y?
In a metre bridge, the gaps are closed by two resistances P and Q and the balance point is obtained at 40 cm. When Q is shunted by a resistance of 10 Ω, the balance point shifts to 50 cm. The values of P and Q are ______

With a resistance of 'X' in the left gap and a resistance of 9 Ω in the right gap of a meter bridge, the balance point is obtained at 40 cm from the left end.
In what way and to which resistance 3 Ω resistance be connected to obtain the balance at 50 cm from the left end?
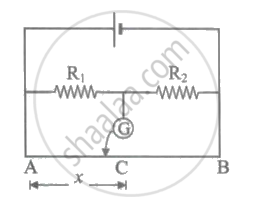
In the metre bridge experiment shown in the figure, the balance length AC corresponding to null deflection of the galvanometer is x. What would be the balance length if the radius of the wire AB is doubled?
On interchanging the resistances, the balance point of a metre bridge shifts to the left by 10 cm. The resistance of their series combination is 1 k`Omega`. How much was the resistance on the left slot before interchanging the resistances?
In Wheatstone's network p = 2 `Omega` , Q = 2 `Omega`, R = 2 `Omega` and S = 3 `Omega`. The resistance with which S is to be shunted in order that the bridge may be balanced is ______.
The resistances in left and right gap of a metrebridge are 20 `Omega` and 30 `Omega` respectively. When the resistance in the left gap is reduced to half its value, the balance point shifts by ______.
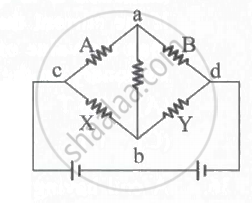
In the Wheatstone bridge, (shown in the figure) X = Y and A > B. The direction of the current between a and b will be ____________.
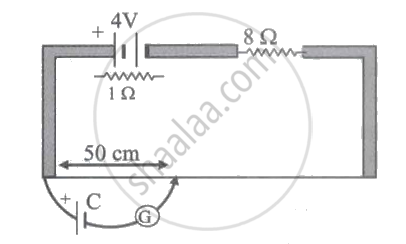
What is the e.m.f of the cell C in the circuit shown in figure, if the deflection in the galvanometer is zero, the resistance of the wire is 3 `Omega`, The length of the wire is 100 cm?
When the value of R in the balanced Wheatstone bridge, shown in the figure, is increased from 5 `Omega` to 7 `Omega`, the value of s has to be increased by 3 `Omega` in order to maintain the balance. What is the initial value of S?
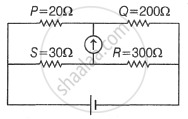
In following figure, a current of 1.4 A flows towards the bridge circuit. The current in 2 n resistor is ______.
The potential difference between the points A and B in the electric circuit shown is ______.

Which among the following resistances can be determined by a metre bridge?
In the measurement of a resistance by the Wheatstone bridge, the known and the unknown resistance are interchanged to eliminate ____________.
Two resistances prepared from the wire of the same material having diameters in the ratio 2 : 1 and lengths in the ratio 2 : 1 are connected in the left gap and right gap of Wheatstone's meter bridge respectively. The distance of the null point from the left end of the wire is ______
In a balanced metre bridge, 5 Ω is connected in the left gap and R Ω in the right gap. When R Ω is shunted with equal resistance, the new balance point is at 1.6 I1 where 'I1' is the earlier balancing length. The value of 'I1' is ______
In a meter bridge experiment, to minimize an error due to contact resistance, ______
In a metre bridge experiment, the ratio of the left-gap resistance to right gap resistance is 2: 3. The balance point from the left is ______.
The resistances in left and right gap of a meter-bridge are 3 `Omega` and 5 `Omega` respectively. When the resistance in the left gap is increased by 10%, the balance point shifts nearly by ______.
When an unknown resistance 'X' is connected in the left gap of a meter bridge and a known resistance 'R' in the right gap, a null point is obtained at 40 cm from the left end. If a 2 Ω resistance is connected in series with 'X' the null point shifts towards the right by 10 cm, with some resistance in the right gap. The value of 'X' must be ______
The Wheatstone bridge is in a more balanced state when the ratio of arms P and Q is ______
The measurement of an unknown resistance R is to be carried out using Wheatstones bridge (figure). Two students perform an experiment in two ways. The first students takes R2 = 10 Ω and R1 = 5 Ω. The other student takes R2 = 1000 Ω and R1 = 500 Ω. In the standard arm, both take R3 = 5 Ω. Both find R = `R_2/R_1 R_3` = 10 Ω within errors.
- The errors of measurement of the two students are the same.
- Errors of measurement do depend on the accuracy with which R2 and R1 can be measured.
- If the student uses large values of R2 and R1, the currents through the arms will be feeble. This will make determination of null point accurately more difficult.
- Wheatstone bridge is a very accurate instrument and has no errors of measurement.
A resistance of 20 Ω is connected in the left gap of a meter bridge and an unknown resistance greater than 20 Ω is connected in the right gap. When these resistances are interchanged, the balance point shifts by 20 cm. The unknown resistance is ______.
The figure below shows a balanced Wheatstone network. If it is disturbed by changing P to 22Ω, then which of the following steps will bring the bridge again to a balanced state?
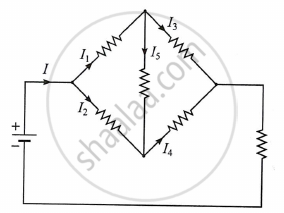
In the given circuit, if I = 100 mA and I1 = I4 = 60 mA, the currents I3 and I5 are ______.
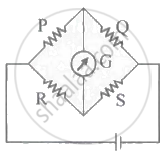
Explain the use of Wheatstone's metre bridge to determine an unknown resistance.
Draw a neat labelled diagram to determine unknown resistance using a meter bridge.
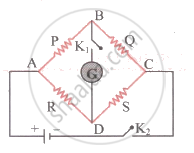
Draw a neat labelled diagram of Kelvin's meter bridge circuit for the measurement of galvanometer resistance.
Find the radius of the wire of length 25m needed to prepare a coil of resistance 25Ω. (Resistivity of material of wire is 3.142 x 10-7Ωm)
Four resistances 4Ω, 4Ω, 4Ω and 12Ω form a Wheatstone's network. Find the resistance which when connected across the 12Ω resistance will balance the network.
What is a post office box? How is the· unknown resistance measured using a post office box?
In the given Wheatstone's network, what should be the value of R for the network to be balanced?
