Advertisements
Advertisements
प्रश्न
Study the given figure and identify the following triangles.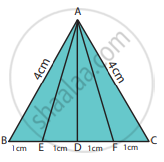
(a) equilateral triangle
(b) isosceles triangles
(c) scalene triangles
(d) acute triangles
(e) obtuse triangles
(f) right triangles
उत्तर
(a) BC = 1 + 1 + 1 + 1 = 4 cm
AB = AC = 4 cm
∆ABC is an equilateral triangle.
(b) ∆ABC and ∆AEF are isosceles triangles.
Since AB = AC = 4 cm
Also AE = AF.
(c) In a scalene triangle, no two sides are equal.
∆AEB, ∆AED, ∆ADF, ∆AFC, ∆ABD, ∆ADC, ∆ABF and ∆AEC are scalene triangles.
(d) In an acute-angled triangle all the three angles are less than 90°
∆ABC, ∆AEF, ∆ABF and ∆AEC are acute-angled triangles.
(e) In an obtuse-angled triangle any one of the angles is greater than 90°
∆AEB and ∆AFC are obtuse angled triangles.
(f) In a right triangle, one of the angles is 90°
∆ADB, ∆ADC, ∆ADE and ∆ADF are right-angled triangles.
APPEARS IN
संबंधित प्रश्न
Two angles of the triangle are given. Find the third angle.
80°, 60°
Two angles of the triangle are given. Find the third angle.
52°, 68°
Two angles of the triangle are given. Find the third angle.
50°, 90°
Two angles of the triangle are given. Find the third angle.
120°, 30°
Using the given information, write the type of triangle in the table given below
| S.No | ∠1 | ∠2 | ∠3 | Type of triangle based on angles | Type of triangle based on sides |
| i. | 60° | 40° | 80° | Acute angled triangle. | Scalene Triangle |
| ii. | 50° | 50° | 80° | ||
| iii. | 45° | 45° | 90° | ||
| iv. | 55° | 45° | 80° | ||
| v. | 75° | 35° | 70° | ||
| vi. | 60° | 30° | 90° | ||
| vii. | 25° | 64° | 91° | ||
| viii. | 120° | 30° | 30° |
If two sides of a triangle are 5 cm and 9 cm, then the third side is ________
Which of the following is not possible?
Is a triangle possible with the angles 90°, 90° and 0°? Why?
State the following statement is true or false? Why?
Every equilateral triangle is an isosceles triangle
Complete the following table:
| Types of Triangle/Its Angles | Acute angled triangle | Right angled triangle | Obtuse angled triangle |
| Any two angles | Always acute angles | i. | Always acute angles |
| Third angle | ii. | Right angle | iii. |
