Advertisements
Advertisements
प्रश्न
The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45° respectively. Find the height of the multi-storeyed building and the distance between the two buildings. (use `sqrt3` = 1.73)
उत्तर
Let AD be the multi-storied building of height h m.
And angle of depression of the top and bottom are 30° and 45°.
We assume that BE = 8, CD = 8 and BC = x, ED = x and AC = h − 8.
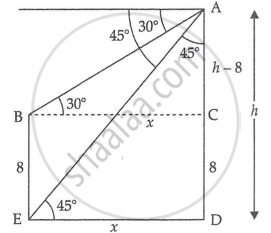
In `triangle`AED,
⇒ tan 45° = `(AD)/(DE)`
⇒ 1 = `h/x`
⇒ h = x
Also, In `triangle`ABC,
⇒ tan 30° = `(AC)/(BC)`
⇒ `1/sqrt3 = ((h − 8))/x`
⇒ x = `hsqrt3 − 8sqrt3`
⇒ h = `hsqrt3 − 8sqrt3` ...[As h = x]
⇒ h = `(8sqrt3)/(sqrt3 - 1)`
On simplifying,
⇒ h = `4(3 + sqrt3)` m And x = `4(3 + sqrt3)` m
So, the height of multi-storied building is `4(3 + sqrt3)` m and the distance between two buildings is `4(3 + sqrt3)` m
