Question

The circumference of a circle, with center O, is divided into three arcs APB, BQC, and CRA such that:
`"arc APB"/2 = "arc BQC"/3 = "arc CRA"/4`

Find ∠BOC.

Answer 1

From the given conditions given in the question
We can draw the circle with arc APB, arc BQC, and arc CRA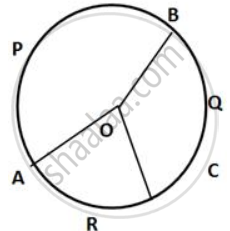

The given equation is
`"arc APB"/2 = "arc BQC"/3 = "arc CRA"/4`
Let 
`"arc APB"/2 = "arc BQC"/3 = "arc CRA"/4` = k ( say )
then 
Arc APB = 2k, Arc BQC = 3k, Arc CRA = 4k
or
Arc APB : Arc BQC : Arc CRA = 2 : 3 : 4
⇒ ∠AOB : ∠BOC : ∠AOC = 2 : 3 : 4
and therefore,
and ∠AOB = 2k°, ∠BOC = 3k°, and ∠AOC = 4k°
Now,
Angle in a circle is 360°
So, 2k + 3k + 4k = 360°
⇒ 9k = 360°
⇒ k = 40°
Hence,
∠BOC = 3 x 40° = 120°.