Question

The differential equation of the family of circles touching Y-axis at the origin is ______.

विकल्प

• `(x^2 + y^2) dy/dx - 2xy` = 0

• `(x^2 - y^2)  + 2xy dy/dx` = 0

• `(x^2 - y^2) dy/dx - 2xy` = 0

• `(x^2 + y^2) dy/dx + 2xy` = 0

Answer 1

The differential equation of the family of circles touching Y-axis at the origin is `underlinebb((x^2 - y^2)  + 2xy dy/dx = 0)`.

Explanation:

Let centre of circle on the X-axis be (K, 0).

∴ The radius of circle will be K.

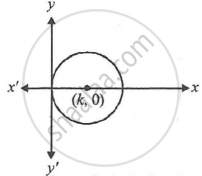
∴ The equation of circle having a centre (K, 0) and radius K is

(x – K)² + (y – 0)² = K²

`\implies` x² + K² – 2hx + y² = K²

`\implies` x² – Kx + y² = 0  ...(i)

On differentiating both sides w.r.t x, we get

`2x - 2K + 2y dy/dx` = 0

`\implies` K = `x + y dy/dx`  ...(ii)

From equations (i) and (ii) we get

`x^2 - 2(x + y dy/dx) x + y^2` = 0

`\implies - x^2 + y^2 - 2xy dy/dx` = 0

`\implies (x^2 - y^2) + 2xy dy/dx` = 0