Advertisements
Advertisements
प्रश्न
The distance of the image of a point (or an object) from the line of symmetry (mirror) is ______ as that of the point (object) from the line (mirror).
उत्तर
The distance of the image of a point (or an object) from the line of symmetry (mirror) is same as that of the point (object) from the line (mirror).
Explanation:
The distance of the image of a point from the line of symmetry is same as that of the point from the line.
APPEARS IN
संबंधित प्रश्न
Complete the following table:
| Point | Reflection in | ||
| x-axis | y-axis | origin | |
| (i) (8, 2) | |||
| (ii) (5, 6) | |||
| (iii) (4, −5) | |||
| (iv) (6, −2) | |||
| (v) (−3, 7) | |||
| (vi) (−4, 5) | |||
| (vii) (−2, −7) | |||
| (viii) (−6, −3) | |||
| (ix) (4, 0) | |||
| (x) (−7, 0) | |||
| (xi) (0, −6) | |||
| (xii) (0, 7) | |||
| (xiii) (0, 0) | |||
Each of the points A (3, 0), B (7, 0), C (- 8, 0), D (- 7, 0) and E (0, 0) is reflected in x-axis to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Each of the points A (0, 7), B (8, 0), C (0, − 5), D (− 7, 0) and E (0, 0) are reflected in origin to points A’, B’, C’, D’ and E’ respectively. Write the co-ordinates of each of the image points A’, B’, C’, D’ and E’.
Construct a triangle XYZ, in which XY = YZ = ZX = 4.5 cm. Draw all its lines of symmetry.
Draw the line(s) of symmetry for the figure drawn below:
Does your windmill look the same on `1/4` of the turn?
Find the number of lines of symmetry in the following shapes. How will you check your answers?

Copy the following drawing on squared paper. Complete such that the resulting figure has two dotted lines as two lines of symmetry.
How did you go about completing the picture?
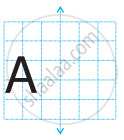
In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e. which letters look the same in the image) and which do not. Can you guess why?
 |
 |
Try for O E M N P H L T S V X
Mirror reflection leads to symmetry always.
