Advertisements
Advertisements
प्रश्न
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
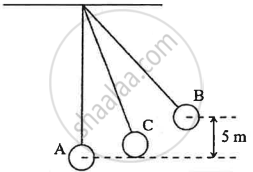
- What is the potential energy of the pendulum at the position B?
- What is the total mechanical energy at point C?
- What is the speed of the bob at the position A when released from position B?
(Take g = 10 ms-2, given that there is no loss of energy.)
उत्तर
- U = mgh = 0.2 × 10 × 5
U = 10 J - According to the rule of conservation of mechanical energy, mechanical energy is constant wherever the pendulum's bob rotates.
∴ Mechanical energy at point C = 10 J - By principle of conservation of energy
U at the top = K at the bottom
∴ `10 = 1/2 xx 0.2 xx v^2`
∴ v2 = 100
∴ v = 10 m s-1
APPEARS IN
संबंधित प्रश्न
A pendulum is oscillating on either side of its rest position. Explain the energy changes that takes place in the oscillating pendulum. How does the mechanical energy remains constant in it? Draw the necessary diagram.
A pendulum with bob of mass m is oscillating on either side from its resting position A between the extremes B and C at a vertical height h and above A. What is the kinetic energy K and potential energy U when the pendulum is at position?
- A,
- B and
- C
The bob of a simple pendulum is imparted a velocity 5 m s-1 when it is at its mean position. To what maximum vertical height will it rise on reaching to its extreme position if 60% of its energy is lost in overcome friction of air? (Take g = 10 m s-2)
Name the type of energy possessed by the bob of a simple pendulum when it is at
- the extreme position,
- the mean position, and
- between the mean and extreme positions.
