Advertisements
Advertisements
प्रश्न
The friction coefficient between a road and the type of a vehicle is 4/3. Find the maximum incline the road may have so that once had brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5 m.
उत्तर
Given,
initial velocity of the vehicle, u = 36 km/h = 10 m/s
final velocity of the vehicle, v = 0
s = 5m, μ = `4/3`, g = 10 m/s2
Let the maximum angle of incline be θ.
Using the equation of motion
`a=(v^2-u^2)/(2s)=(0-10)/(2xx5)`
= -10 m/s2
From the free body diagram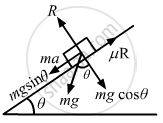
R − mg cos θ = 0
⇒ R = mg cos θ (1)
Again,
ma + mg sin θ − μ R = 0
⇒ ma + mg sin θ − μmg cos θ = 0
⇒ a + g sin θ − μg cos θ = 0
`=>10+10sintheta-(4/3)xx10cos theta = 0`
⇒ 30 + 30 sin θ − 40 cos θ = 0
⇒ 3 + 3 sin θ − 4 cos θ = 0
⇒ 4 cos θ − 3 sin θ = 3
`=>4sqrt(1-sin^2theta)` = 3 + 3 sin θ
On squaring, we get
16 (1 − sin2 θ) = 9 + 9 sin2 θ + 18 sin θ
25 sin2 θ + 18 sin θ − 7 = 0
`=> sintheta=(18+sqrt(18^2-4(25)(-7)))/(2x25)`
`=(-18+32)/50=14/50=0.28` (Taking positive sign only)
⇒ θ = sin-1 (0.28) = 16°
Therefore, the maximum incline of the road, θ = 16°.
APPEARS IN
संबंधित प्रश्न
A body of mass M is kept on a rough horizontal surface (friction coefficient = μ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
A boy of mass M is applying a horizontal force to slide a box of mass M' on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
The contact force exerted by a body A on another body B is equal to the normal force between the bodies We conclude that
(a) the surface must be frictionless
(b) the force of friction between the bodies is zero
(c) the magnitude of normal force equal that of friction
(d) the bodies may be rough but they don't slip on each other.
Mark the correct statements about the friction between two bodies.
(a) Static friction is always greater than the kinetic friction.
(b) Coefficient of static friction is always greater than the coefficient of kinetic friction.
(c) Limiting friction is always greater than the kinetic friction.
(d) Limiting friction is never less than static friction.
A block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
(a) The graph is a straight line of slope 45°.
(b) The graph is a straight line parallel to the F-axis.
(c) The graph is a straight line of slope 45° for small F and a straight line parallel to the F-axis for large F.
(d) There is a small kink on the graph.
A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s2. What is the coefficient of kinetic friction between the block and the plane?
Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of the block is 4 kg.
Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
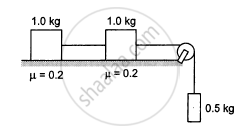
Consider the situation shown in the following figure. Calculate (a) the acceleration of the 1.0 kg blocks, (b) the tension in the string connecting the 1.0 kg blocks and (c) the tension in the string attached to 0.50 kg.
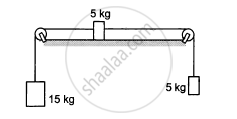
The friction co-efficient between the table and the block shown in the following figure is 0.2. Find the tensions in the two strings.
The friction coefficient between an athelete's shoes and the ground is 0.90. Suppose a superman wears these shoes and races for 50 m. There is no upper limit on his capacity of running at high speeds. (a) Find the minimum time that he will have to take in completing the 50 m starting from rest. (b) Suppose he takes exactly this minimum time to complete the 50 m, what minimum time will he take to stop?
A block of mass M is kept on a rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
The friction coefficient between the two blocks shown in the following figure is μ but the floor is smooth. (a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system? (b) Suppose the horizontal force applied is double of that found in part (a). Find the accelerations of the two masses.
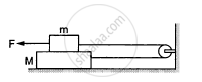
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
Consider the situation shown in the following figure. Suppose a small electric field E exists in the space in the vertically charge Q on its top surface. The friction coefficient between the two blocks is μ but the floor is smooth. What maximum horizontal force F can be applied without disturbing the equilibrium?
[Hint: The force on a charge Q bye the electric field E is F = QE in the direction of E.]
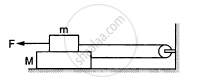
Find the acceleration of the block of mass M in the situation of figure in the following. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
