Advertisements
Advertisements
प्रश्न
The heavier block in an Atwood machine has mass twice that of the lighter one. The tension in the string is 16⋅0 N when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest.
उत्तर
\[\text{ Given } , \]
\[\text{ Tension in the string, T = 16 N } \]
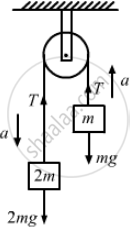
\[\text{ From the free - body diagrams, } \]
\[\text{ T - 2 mg + 2 ma = 0 . . . (i) } \]
\[\text{ T - mg - ma = 0 . . . (ii) } \]
\[\text{ From equations (i) and (ii), } \]
\[\text{ T = 4 ma } \]
\[ \Rightarrow a = \frac{T}{4\text{m}} = \frac{4}{\text{m}} \text{ m/ s } ^2\]
\[\text{ Now, S = ut }+ \frac{1}{2}\text{ at}^2 \]
\[ = \left( \frac{1}{2} \right) \times \frac{4}{\text{m}} \times 1 \left[ \text{as u } = 0 \right]\]
\[ = \left( \frac{2}{\text{ m } } \right)\]
\[\text{ Net mass = 2 m - m = m } \]
\[\text{ Decrease in potential energy, } \]
\[ \text{ P . E . = mgh} \]
\[ = \text{ m }\times \text{ g } \times \left( \frac{2}{\text{ m }} \right)\]
\[ = 9 . 8 \times 2 = 19 . 6 \text{ J} \]
