Advertisements
Advertisements
प्रश्न
The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.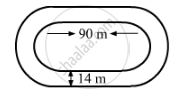
उत्तर
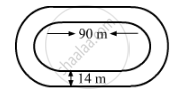
It is given that the inside perimeter of the running track is 400 m . It means the length of the inner track is 400 m .
Let r be the radius of the inner semicircles .
Observe: Perimeter of the inner track = Length of two straight portions of 90 m + Length of two semicircles
∴ 400 = (2 x 90) + (2 x Perimiter of a semicircle)
\[400 = 180 + (2 \times \frac{22}{7} \times r)\]
\[400 - 180 = (\frac{44}{7} \times r)\]
\[\frac{44}{7} \times r = 220\]
\[r = \frac{220 \times 7}{44} = 35 m\]
∴ Width of the inner track = 2r = 2 x 35 = 70 m
Since the track is 14 m wide at all places, so the width of the outer track: 70 + (2 x 14) = 98 m
∴ Radius of the outer track semicircles \[= \frac{98}{2} = 49 m\]
Area of the outer track = (Area of the rectangular portion with sides 90 m and 98 m) + (2 x Area of two semicircles with radius 49 m)
\[ = (98 \times 90) + (2 \times \frac{1}{2} \times \frac{22}{7} \times {49}^2 )\]
\[ = (8820) + (7546)\]
\[ = 16366 m^2 \]
And, area of the inner track = (Area of the rectangular portion with sides 90 m and 70 m) + (2 x Area of the semicircle with radius 35 m)
\[ = (70 \times 90) + (2 \times \frac{1}{2} \times \frac{22}{7} \times {35}^2 )\]
\[ = (6300) + (3850)\]
\[ = 10150 m^2 \]
∴ Area of the running track = Area of the outer track - Area of the inner track
\[ = 16366 - 10150\]
\[ = 6216 m^2 \]
And, length of the outer track = (2 x length of the straight portion) + (2 \times perimeter of the semicircles with radius 49 m)
\[ = (2 \times 90) + (2 \times \frac{22}{7} \times 49)\]
\[ = 180 + 308\]
\[ = 488 m\]
APPEARS IN
संबंधित प्रश्न
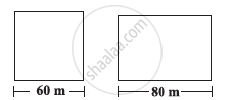
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
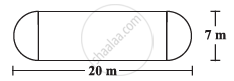
The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of the garden [Length of rectangle is 20 − (3.5 + 3.5) metres]
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food − piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.

A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. 20.23. If AB = 60 m and BC = 28 m, find the area of the plot.
A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = 22/7).
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.
The length and breadth of a rectangular field are in the ratio 7 : 4. If its perimeter is 440 m, find its length and breadth. Also, find the cost of fencing it @ ₹150 per m.
A wire is in the shape of square of side 20 cm. If the wire is bent into a rectangle of length 24 cm, find its breadth.
The area of a parallelogram is 60 cm2 and one of its altitudes is 5 cm. The length of its corresponding side is ______.
