Advertisements
Advertisements
प्रश्न
The length and the breadth of a conference hall are in the ratio 7: 4 and its perimeter is 110 m. Find:
(i) area of the floor of the hall.
(ii) a number of tiles, each a rectangle of size 25 cm x 20 cm, required for the flooring of the hall.
(iii) the cost of the tiles at the rate of ₹ 1,400 per hundred tiles.
उत्तर
Ratio in length and breadth = 7 : 4
Perimeter = 110 m
∴ Length + Breadth = `110/2 = 55` m
Sum of ratios = 7 + 4 = 11
∴ Length = `(55 xx 7)/11 = 35` m
and breath = `(55 xx 4)/11 = 20` m
(i)
Area of floor = l × b
= `35 xx 20 = 700 "m"^2`
(ii)
Size of tile = 25 cm × 20 cm
= `(25 xx 20)/(100 xx 100)`
= `1/20 "m"^2`
∴ Number of tiles
= `"Area of floor"/"Area of one tile"`
= `(700 xx 20)/1 = 14000`
(iii)
Cost of tiles = ₹ 1400 per 100 tiles
∴ Total cost = `(14000 xx 1400)/100`
= ₹ 196000
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangle is 34 cm. If its breadth is 16 cm; find its :
(i) length
(ii) area
The length of a rectangle is 16 cm and its perimeter is equal to the perimeter of a square with side 12.5 cm. Find the area of the rectangle.
A rectangle with length = 18 cm and breadth = 12 cm has same perimeter as that of a regular pentagon. Find the side of the pentagon.
Each side of a square is 45 cm and a rectangle has length 50 cm. If the perimeters of both (square and rectangle) are same, find the breadth of the rectangle.
The sides of a triangle are 24.7cm, 20.4 cm, and 10.5 cm respectively. What is the perimeter of the triangle?
How many different rectangles can be made with a 48 cm long string? Find the possible pairs of length and breadth of the rectangles.
Find the perimeter of the following figure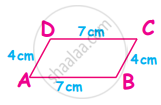

Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.
Which of these rectangles has the longest perimeter?
Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.
In the given figure, perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).
 |
 |
| (i) | (ii) |
