Advertisements
Advertisements
प्रश्न
The length of a rectangle is two times its breadth. Its perimeter is 60 cm.
- If the breadth of rectangle is x cm, the length of the rectangle is ______.
- Perimeter in terms of x is ______.
- The equation formed is ______.
- The solution of the equation is ______.
उत्तर
- If the breadth of rectangle is x cm, the length of the rectangle is 2x.
- Perimeter in terms of x is 6x.
- The equation formed is 6x = 60.
- The solution of the equation is 10.
Explanation:
a. It is given that the length of the rectangle is two times its breadth.
∴ Length = 2x cm
b. Perimeter of rectangle = 2(Length + Breadth) = 2(2x+ x)
⇒ 2(3x) = 60
⇒ 6x = 60
c. As per the condition given in the question, perimeter is 60 cm
The equation formed is, 4x + 2x = 60
6x = 60
d. On dividing the equation by 6, we get
`(6x)/6 = 60/6`
⇒ x = 10
Hence, the solution of the equation is 10.
APPEARS IN
संबंधित प्रश्न
Set up equation and solve them to find the unknown number in the following case:
If I take three-fourths of a number and add 3 to it, I get 21.
The length of a rectangle is two times its breadth. Its perimeter is 60 cm.
The solution of the equation is ______.
In a bag there are 5 and 2 rupee coins. If they are equal in number and their worth is ₹ 70, then
There are ______ 5 rupee coins and ______ 2 rupee coins.
In a Mathematics quiz, 30 prizes consisting of 1st and 2nd prizes only are to be given. 1st and 2nd prizes are worth ₹ 2000 and ₹ 1000, respectively. If the total prize money is ₹ 52,000 then show that:
The equation formed is ______.
A number divided by 2 and then increased by 5 is 9.
A number when divided by 6 gives the quotient 6. What is the number?
The perimeter of a rectangle is 40 m. The length of the rectangle is 4 m less than 5 times its breadth. Find the length of the rectangle.
The length of a rectangle is two times its width. The perimeter of the rectangle is 180 cm. Find the dimensions of the rectangle.
Follow the directions and correct the given incorrect equation, written in Roman numerals:
Remove two of these matchsticks to make a valid equation:

The three scales below are perfectly balanced if • = 3. What are the values of ∆ and * ?
| (a) |  |
| (b) | 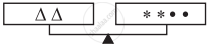 |
| (c) | 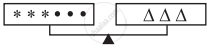 |
