Question

The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is ______.

विकल्प

• `sqrt(1 + sin(A/2))`

• `sqrt(1 + cos(A/2))`

• `sqrt(1 + tan^2(A/2))`

• `sqrt(1 + cot^2(A/2))`

Answer 1

The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is `underlinebb(sqrt(1 + cot^2(A/2)))`.

Explanation:

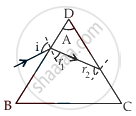
If the angle of incidence on face DC, or r₂, is greater than the critical angle θ_C for the maximum angle of incidence (i₁ = 90° = maximum) at face DB, a ray of light will not exit the prism for any value of the angle of incidence provided.

At DB, 1 × sin90° = μ sinr₁

⇒ `r_1 = sin^-1(1/mu)`

or `r_1 = theta_C` .............(i)

For no emergence

r₂ > θ_C ................(ii)

Adding equations (i) and (ii),

r₁ + r₂ > 2θ_C   ...(iii)

Also r₁ + r₂ = A ...(iv)

We know that the sum of all angles in any triangle equals 180.

90 – r₁ + 90 – r₂ + A = 180

A = r₁ + r₂

Now, solving equations (iii) and (iv),

A > 2θ_C

⇒ `sin  A/2 > sintheta_C`

µ > cosec `A/2`

As a result, the maximum value of

`mu = cosec  A/2 = sqrt(1 + cot^2  A/2)`