Advertisements
Advertisements
प्रश्न
The perimeter of a rectangle is 46 m and its length is 15 m. Find its :
(i) breadth
(ii) area
(iii) diagonal.
उत्तर
(i)
Perimeter of rectangle = 46 m
length, l = 15 m
2 (l+b) = 46
2(15 + b) = 46
15+b = `46/2` = 23
b = 23 – 15
b = 8 m
(ii)
area = `l xx b = 15 xx 8 = 120 "m"^2`
(iii)
diagonal = `sqrt(l^2 + b^2) = sqrt(15^2 + 8^2)`
= `sqrt(225 + 64) = sqrt(289) = 17`m
Hence (i) 8 m (ii) 120 m2 (iii) 17 m
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangle is 34 cm. If its breadth is 16 cm; find its :
(i) length
(ii) area
The length of a rectangle is 16 cm and its perimeter is equal to the perimeter of a square with side 12.5 cm. Find the area of the rectangle.
Find the perimeter of a rectangle whose:
length = 40 cm and breadth = 35 cm
Each side of a square is 45 cm and a rectangle has length 50 cm. If the perimeters of both (square and rectangle) are same, find the breadth of the rectangle.
The side of a square is 3.6 cm; find its perimeter.
The sides of a triangle are 24.7cm, 20.4 cm, and 10.5 cm respectively. What is the perimeter of the triangle?
Find the perimeter and the area of the rectangle whose length is 6 m and breadth is 4 m
In the given figure, perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).
 |
 |
| (i) | (ii) |
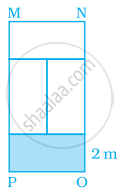
Rectangle MNOP is made up of four congruent rectangles (Figure). If the area of one of the rectangles is 8 m2 and breadth is 2 m, then find the perimeter of MNOP.
In the given figure, a rectangle with perimeter 264 cm is divided into five congruent rectangles. Find the perimeter of one of the rectangles.