Question

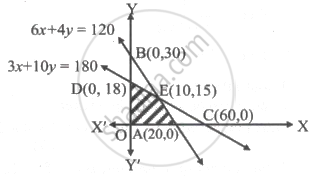
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______ 

विकल्प

• (15, 10)

• (10, 15)

• (0, 18)

• (20, 0)

Answer 1

The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is (10, 15).

Explanation:

The feasible region Lies on the origin side of the lines

6x + 4y = 120 and 3x + 10y = 180

The comer points of feasible region are

O(0, 0), A (20, 0), E (10, 15) and D (0, 18)

∴ The maximum value of 45x + 55y is at E(10, 15)

Max (45x + 55y) = 45(10) + 55(15)

= 1275