Advertisements
Advertisements
प्रश्न
The real number lines for two inequations A and B are as given below, A ∩ B is:


विकल्प
उत्तर

Explanation:
Given

and 
∴ A = {x : x ∈ R, – 3 < x ≤ 1}
B = {x : x ∈ R, – 4 ≤ x < 0}
∴ A ∩ B = – 3 < x < 0
= 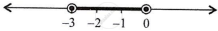
संबंधित प्रश्न
Find the values of x, which satisfy the inequation `-2 5/6 < 1/2 - (2x)/3 ≤ 2, x ∈ W`. Graph the solution set on the number line.
For the following inequations, graph the solution set on the real number line:
– 4 ≤ 3x – 1 < 8
Given that x ∈ I. solve the inequation and graph the solution on the number line:
`3 >= (x - 4)/2 + x/3 >= 2`
Solve the inequation:
`-2 1/2 + 2x <= (4x)/5 <= 4/3 + 2x, x ∈ W`.
Graph the solution set on the number line.
Solve the following in equation write the solution set and represent it on the number line:
`-x/3 <= x/2 -1 1/3 < 1/6, x ∈ R`
Solve the following in equation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ∈ R
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 - 4x ≤ 7 1/2, x ∈ I`
Solve 2(x – 3)< 1, x ∈ {1, 2, 3, …. 10}
Solve : `(4x - 10)/(3) ≤ (5x - 7)/(2)` x ∈ R and represent the solution set on the number line.
For the following real number line, the solution set is:




