Advertisements
Advertisements
प्रश्न
The shadow of a 3 m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24 m long, how tall is the flagstaff?
उत्तर
Let the length of flagstaff is x.
Shadow: Length :: Shadow : Length
4 m : 3 m :: 24 m : x
`4/3 = 24/x` .....`["If a, b, c and d are in proportion" a/b = c/d]`
`4 xx x = 3 xx 24` ......[By cross-multiplication]
`x = (3 xx 24)/4`
`x` = 18
Hence, the flagstaff is 18 m tall.
APPEARS IN
संबंधित प्रश्न
If x and y be unequal and x : y is the duplicate ratio of x + z and y + z, prove that z is mean proportional between x and y.
If a, b, c, d are in continued proportion, prove that (b - c)2 + (c - a)2 + (d - b)2 = (d - a)2.
Find the value of x in the following proportions : x : 50 :: 3 : 2
Verify the following:
60 : 105 : : 84 : 147
In proportion, the 1st, 2nd, and 4th terms are 51, 68, and 108 respectively. Find the 3rd term.
An electric pole casts a shadow of length 20 m at a time when a tree 6 m high casts a shadow of length 8 m. Find the height of the pole.
If `x/a = y/b = z/c`, prove that `"ax - by"/((a + b)(x- y)) + "by - cz"/((b + c)(y - z)) + "cz - ax"/((c + a)(z - x)` = 3
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
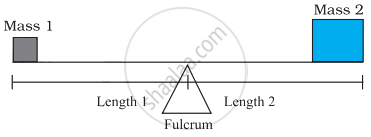
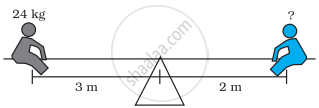
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?
The mean proportional between 4 and 9 is ______.
If 2x, 9 and 18 are in continued proportion, the value of x is ______.
