Advertisements
Advertisements
प्रश्न
The shape of a farm is a quadrilateral. Measurements taken of the farm by naming its corners as P, Q, R, S in order are as follows. l(PQ) = 170 m, l(QR) = 250 m, l(RS) = 100 m, l(PS) = 240 m, l(PR) = 260 m. Find the area of the field in hectare (1 hectare = 10,000 sq. m)
उत्तर
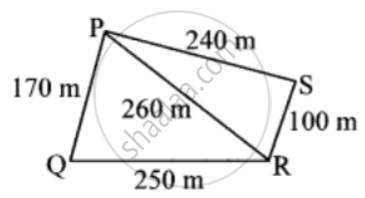
Area of the field = A(∆PQR) + A(∆PSR)
In ∆PQR, a = 170 m, b = 250 m, c = 260 m
Semiperimeter of ∆PQR = s
= `1/2(a + b + c)`
= `1/2(170 + 250 +260)`
= `1/2 xx 680`
= 340
∴ A(ΔPQR) = `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))`
= `sqrt(340(340 - 170)(340 - 250)(340 - 260))`
= `sqrt(340 xx 170 xx 90 xx 80)`
= `sqrt(2 xx 170 xx 170 xx 3 xx 3 xx 10 xx 2 xx 2 xx 2 xx 10)`
= `sqrt(2^2 xx 2^2 xx 3^2 xx 10^2 xx 170^2)`
= 2 × 2 × 3 × 10 × 170
= 20400 sq. m
In ΔPSR, a = 240 m, b = 100 m, c = 260 m
Semiperimeter of ΔPSR = s
= `1/2(240 + 100 + 260)`
= `1/2 xx 600`
= 300
∴ A(ΔPSR)
= `sqrt(300(300 - 240)(300 - 100)(300 - 260))`
= `sqrt (300 xx 60 xx 200 xx 40)`
= `sqrt(5 xx 60 xx 60 xx 5 xx 40 xx 40)`
= `sqrt(5^2 xx 40^2 xx 60^2)`
= 5 × 40 × 60
= 12000 sq. m.
Area of the field = A(∆PQR) + A(∆PSR)
= 20400 + 12000
= 32400 sq. m
= `32400/10000` …[1 hectare = 10,000 sq. m]
= 3.24 hectares
∴ The area of the field is 3.24 hectares.
