Advertisements
Advertisements
प्रश्न
The sum of the first 7 terms of an A.P. is 63 and the sum of its next 7 terms is 161. Find the 28th term of this A.P ?
उत्तर
Let the first term of the A.P. be a and the common difference be d.
nth term of an A.P. is given by a + (n − 1)d.
∴ 7th term of the A.P. = a + 6d
8th term of the A.P. = a + 7d
14th term of the A.P. = a + 13d
Let the sum of the first seven terms of the A.P. be S1-7.
∴ S1-7 = n2">n2n2(First term + Seventh term)
\[\Rightarrow S_{1 - 7} = \frac{7}{2}\left( a + a + 6d \right)\]
\[ \Rightarrow 63 = 7\left( a + 3d \right) \]
\[ \Rightarrow 9 = a + 3d . . . (1)\]
Let the sum of the next seven terms be S8-14.
∴ S8-14 = n2">n2n2(Eighth term + Fourteenth term)
\[ \Rightarrow 161 = 7\left( a + 10d \right)\]
\[ \Rightarrow 23 = a + 10d . . . (2)\]
On subtracting equation (1) from equation (2), we get:
7d = 14
⇒ d = 2
On putting the value of d in equation (1), we get:
a = 9 − 6 = 3
APPEARS IN
संबंधित प्रश्न
The sum first 10 terms of an AP is -150 and the sum of its next 10 terms is -550 . Find the AP.
An AP 5, 12, 19, .... has 50 term. Find its last term. Hence, find the sum of its last 15 terms.
Find the sum of all three digit natural numbers, which are multiples of 7 ?
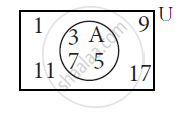
Observe the adjacent Venn diagram and write the complement of A.
Multiply : 2`sqrt(12) × sqrt(3)`
A = {1, 2, 3,4, 5}, B = {5, 6, 7} write AUB .
Write the lower and the uppper class limit of 35 to 40
Find the first four terms in A.P. When a = 10 and d = 3.
Find the value of the determinate:
`|(4,-2),(3,1)|`
Complete the following activity to find the number of natural numbers between 1 and 171, which are divisible by 5:
Activity :

