Advertisements
Advertisements
प्रश्न
The sum of first q terms of an AP is (63q – 3q2). If its pth term is –60, find the value of p. Also, find the 11th term of its AP.
उत्तर १
Let Sq denote the sum of the first q terms of the AP. Then,
Sq = 63q – 3q2
⇒ Sq–1 = 63(q – 1) –3(q – 1)2
= 63q – 63 – 3 (q2 – 2q + 1)
= –3q2 + 69q – 66
Suppose aq denote the qth term of the AP
∴ aq = Sq – Sq–1
= (63q – 3q2) – (3q2 + 69q – 66)
= –6q + 66 ...(1)
Now,
ap = –60 ...(Given)
`\implies` –6p + 66 = –60 ...[From (1)]
`\implies` –6p = –60 – 66 = –126
`\implies` p = 21
Thus, the value of p is 21.
Putting q = 11 in (1), we get
a11 = –6 × 11 + 66 = –66 + 66 = 0
Hence, the 11th term of the AP is 0.
उत्तर २
\[S_q = 63q - 3 q^2 \]
We know
\[ a_q = S_q - S_{q - 1} \]
\[ \therefore a_q = 63q - 3 q^2 - 63\left( q - 1 \right) + 3 \left( q - 1 \right)^2 \]
\[ a_q = 66 - 6q\]
\[\text{ Now}, a_p = - 60\]
\[ \Rightarrow 66 - 6p = - 60\]
\[ \Rightarrow 126 = 6p\]
\[ \Rightarrow p = 21\]
\[ a_{11} = 66 - 6 \times 11 = 0\]
APPEARS IN
संबंधित प्रश्न
Find the sum of first 100 even number which are divisible by 5.
The sum first 10 terms of an AP is -150 and the sum of its next 10 terms is -550 . Find the AP.
Which of the following sequences are A.P.? If they are A.P. find the common difference.
Is the following sequences are A.P.? If is A.P. find the common difference.
0.3, 0.33, 0.333,...
Write the correct number in the given boxes from the following A. P.
1, 8, 15, 22,...
Here a =Here a = t1 =
t1 =  , t2 =
, t2 =  , t3 =
, t3 =  ,
,
t2 – t1 =  –
–  =
= 
t3 – t2 =  –
–  =
=  ∴ d =
∴ d = 
On the world environment day tree plantation programme was arranged on a land which is triangular in shape. Trees are planted such that in the first row there is one tree, in the second row there are two trees, in the third row three trees and so on. Find the total number of trees in the 25 rows.
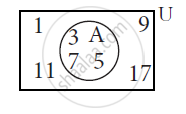
Observe the adjacent Venn diagram and write the complement of A.
Find the class-mark of 80-90.
Write the lower and the uppper class limit of 35 to 40
Find S2 for the A.P. 3,5,7,9,......
