Advertisements
Advertisements
प्रश्न
The sum of the probabilities of all the elementary events of an experiment is _________.
उत्तर
The sum of the probabilities of all the elementary events of an experiment is 1.
APPEARS IN
संबंधित प्रश्न
A child has a die whose six faces shows the letters as given below:
| A | B | C | D | E | A |
The die is thrown once. What is the probability of getting (i) A? (ii) D?
A and B throw a pair of dice. If A throws 9, find B’s chance of throwing a higher number.
A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is Red
In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize?
What is the probability that a number selected at random from the number 1,2,2,3,3,3, 4, 4, 4, 4 will be their average?
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is neither white nor black.
Fill in blank:
Probability of a sure event is...........
Fill in blank:
Every elementary event associated to a random experiment has........... probability.
A game consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
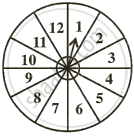
If the outcomes are equally likely, find the probability that the pointer will point at:
- 6
- an even number.
- a prime number.
- a number greater than 8.
- a number less than or equal to 9.
- a number between 3 and 11.
A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a dice, very small in size, is dropped on the rectangular paper without seeing towards it. If the dice falls and lands on the paper only, find the probability that it will fall and land outside the circle.
Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on consecutive day.
In a game of chance, a spinning arrow comes to rest at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8. All these are equally likely outcomes. Find the probability that it will rest at a number greater than 2.

A bag contains 3 red, 3 white and 3 green balls. One ball is taken out of the bag at random. What is the probability that the ball drawn is – either red or white.
Fill in the blank:
The probability of an impossible event is ....... .
Two dice are thrown simultaneously. Find the probability of getting: a multiple of 3 as the sum.
Two dice are thrown at the same time. Find the probability of getting different numbers on both dice.
Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is 6
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. Determine the probability that the card is a heart.
The king, queen and jack of clubs are removed from a deck of 52 playing cards and then well shuffled. Now one card is drawn at random from the remaining cards. What is the probability that the card is 10 of hearts?
The table given below shows the months of birth of 36 students of a class:
| Month of birth |
Jan. | Feb. | Mar. | Apr. | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
| No. of students |
4 | 3 | 5 | 0 | 1 | 6 | 1 | 3 | 4 | 3 | 4 | 2 |
A student is choosen at random. Fill in the boxes.
Total number of students = `square`
Let E be the event that the selected student is born in June.
Then,
Number of times event E occurs = `square`
So, P (selected student is born in June)
P(E) = `"Number of students born in June"/square`
= `square/square`
= `square`
