Question

Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is

विकल्प

• `G m^2/r^2`

• `(Gm^2)/(4r^2)`

• `sqrt(2) (Gm^2)/(4r^2)`

• `sqrt(3) (Gm^2)/(4r^2)`

Answer 1

`sqrt(3) (Gm^2)/(4r^2)`

Explanation:

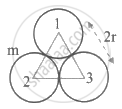
Force om 1^st sphere `vecF_1 = vecF_12 + vecF_13`

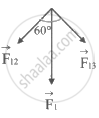
Now, `|vecF_12| = |vecF_13| = (GM^2)/(2r)^2 = (Gm^2)/(4r^2)`

The resultant of the attractive forces `vecF_12` and `vecF_13` is determined by the parallelogram law of vectors since they point in opposing directions.

∴ F₁ = `sqrt(F_12^2 + F_13^2 + 2F_12F_13 cos theta)`

∴ F₁ = `sqrt(2F_12^2 + 2F_12^2 cos 60^circ)`

∴ F₁ = `sqrt(2F_12^2 + F_12^2)`  .....(∵ cos 60° = 1/2)

∴ F₁ = `sqrt(3)` F₁₂

∴ F₁ = `sqrt(3) (Gm^2)/(4r^2)`

Because of the symmetry of the design, each sphere will experience equal magnitude force.