Advertisements
Advertisements
प्रश्न
Try to construct triangles using match sticks. Some are shown here.
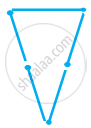 |
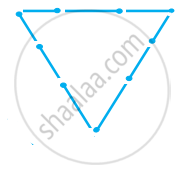 |
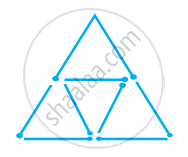 |
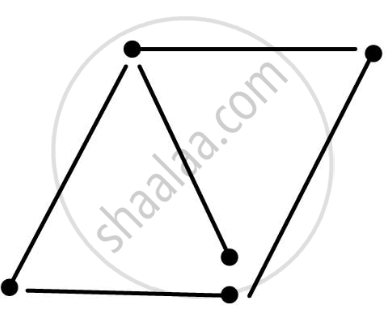
Can you make a triangle with 5 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
उत्तर
This is an acute angle triangle and it is possible to make a triangle with five matchsticks, in this case, sum of two sides is greater than third side.
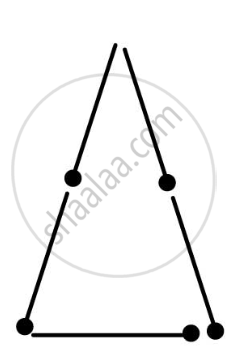 |
 |
APPEARS IN
संबंधित प्रश्न
Construct traingle ABC, when: BC = 3 cm, AC = 4 cm and AB = 5 cm. Measure angle ACB. Give a special name to this triangle.
If each of the two equal angles of an isosceles triangle is 68°, find the third angle.
The angles of a triangle are in the ratio 3:5: 7. Find each angle.
The angles of a triangle are (2x – 30°),(3x – 40°) and ( x + 10°) Find the value of x .
Construct a triangle ABC given AB = 6 cm, BC = 5 cm and CA = 5.6 cm. From vertex A draw a perpendicular on to side BC. Measure the length of this perpendicular.
Construct a triangle ABC given BC = 5 cm, AC = 6 cm and ∠C = 75°. Draw the bisector of the interior angle at A. Let this bisector meet BC at P ; measure BP
Observe the figure below and write the type of the triangle based on its angles.

Δ XYZ is ... triangle
Observe the figure below and write the type of the triangle based on its angles.
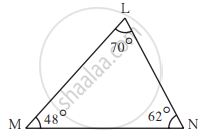
Δ LMN is ... triangle
Match the following:
|
|
Measures of Triangle |
|
Type of Triangle |
| (i) | 3 sides of equal length | (a) | Scalene |
| (ii) | 2 sides of equal length | (b) | Isosceles right angled |
| (iii) | All sides are of different length | (c) | Obtuse angled |
| (iv) | 3 acute angles | (d) | Right angled |
| (v) | 1 right angle | (e) | Equilateral |
| (vi) | 1 obtuse angle | (f) | Acute angled |
|
(vii) |
1 right angle with two sides of equal length |
(g) | Isosceles |
Try to construct triangles using match sticks. Some are shown here.
 |
 |
 |
Can you make a triangle with 6 matchsticks?
(Remember you have to use all the available matchsticks in each case) Name the type of triangle in each case. If you cannot make a triangle, think of reasons for it.
