Advertisements
Advertisements
प्रश्न
Two Navy helicopters A and B are flying over the Bay of Bengal at saine altitude from sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10 km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B
उत्तर
A, B are the positions of the helicopter above the sea level.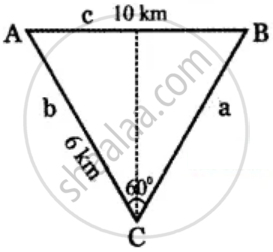
Distance between A and B = 10 km
C – Position of the boat on the surface of sea.
AC, BC are the directions of the boat as seen from A and B respectively.
Distance of the boat C from A = 6 k.m
∠ACB = 60°
Using cosine formula
AB2 = BC2 + AC2 – 2 BC . AC cos ∠ACB
c2 = a2 + b2 – 2ab cos C
102 = a2 + 62 – 2a × 6 cos 60°
100 = `"a"^2 + 36 - 12"a"(1/2)`
0 = a2 + 36 – 6a – 100
a2 – 6a – 64 = 0
a = `(6 +- sqrt(36 - 4(1)(- 64)))/(2 xx 1)`
= `(6 +- sqrt(36 + 256))/2`
= `(6 +- sqrt(292))/2`
= `(6 +- sqrt(4 xx 73))/2`
a = `(6 +- 2sqrt(73))/2`
= `3 +- sqrt(73)`
a = `3 + sqrt(73)` or a = `3 - sqrt(73)`
a = `3 - sqrt(73)` is not possible.
∴ a = `3 + sqrt(73)` km
APPEARS IN
संबंधित प्रश्न
Determine whether the following measurements produce one triangle, two triangles or no triangle:
∠B = 88°, a = 23, b = 2. Solve if solution exists
If the sides of a ∆ABC are a = 4, b = 6 and c = 8, then show that 4 cos B + 3 cos C = 2
In a ∆ABC, if a = `sqrt(3) - 1`, b = `sqrt(3) + 1` and C = 60° find the other side and other two angles
In any ∆ABC, prove that the area ∆ = `("b"^2 + "c"^2 - "a"^2)/(4 cot "A")`
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm
Two soldiers A and B in two different underground bunkers on a straight road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5km apart, find the distance of the intruder from B
A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the westernmost point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km, and ∠APB = 120°, then find the length of the tunnel to be built
A fighter jet has to hit a small target by flying a horizontal distance. When the target is sighted, the pilot measures the angle of depression to be 30°. If after 100 km, the target has an angle of depression of 45°, how far is the target from the fighter jet at that instant?
A plane is 1 km from one landmark and 2 km from another. From the plane’s point of view, the land between them subtends an angle of 45°. How far apart are the landmarks?
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A = 60° and ∠B = 45°, AC = 4 km in the ∆ABC. Find the total distance he covered during his morning walk
Suppose that a satellite in space, an earth station, and the centre of earth all lie in the same plane. Let r be the radius of earth and R he the distance from the centre of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite, If the line segment connecting the earth station and satellite subtends angle α at the centre of earth then prove that d = `"R"sqrt(1 + ("r"/"R")^2 - 2 ("r"/"R") cos alpha)`
Choose the correct alternative:
In a triangle ABC, sin2A + sin2B + sin2C = 2, then the triangle is
Choose the correct alternative:
The triangle of maximum area with constant perimeter 12m
