Advertisements
Advertisements
प्रश्न
उदाहरण सहित निम्नलिखित के बीच का अंतर को स्पष्ट कीजिए:
- किसी समय अंतराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है)। और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई।
- किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वार विभाजित की गई कुल पथ-लंबाई के रूप में परिभाषित किया जाता है)।प्रदर्शित कीजिए कि (a) व (b) दोनों में हीं दूसरी राशि पहली से अधिक या उसके बराबर है । समता का चिह्न कब सत्य होता है ? (सरलता के लिए केवल एकबिमीय गति पर विचार कीजिए।)
उत्तर
- विस्थापन का परिमाण एक कण की गति के दौरान उसके प्रारंभिक और अंतिम बिंदुओं के बीच की सबसे छोटी दूरी होती है, जबकि कुल पथ की लंबाई उस दौरान कण द्वारा तय की गई वास्तविक दूरी होती है। यदि एक कण A से B तक और फिर B से C तक जाता है, जैसा कि दिखाया गया है,
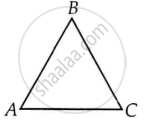
विस्थापन का परिमाण AC की दूरी के बराबर होता है।
कुल पथ की लंबाई = दूरी AB + दूरी BC
चित्र से हम देख सकते हैं कि कुल पथ की लंबाई (AB + BC) विस्थापन के परिमाण (AC) से अधिक है। यदि कण की गति एक आयाम में हो, अर्थात् सीधी रेखा में, तो दी गई समयावधि के लिए कुल पथ की लंबाई विस्थापन के परिमाण के बराबर होती है। - `"औसत वेग का परिमाण" = "विस्थापन का परिमाण" / "समय अंतराल"`
दिए गए कण के लिए।
`"औसत वेग" = ("AC")/"t"`
`"औसत चाल" = "कुल दूरी" / "कुल समय"`
`= ("AB"+"BC")/"t"`
चूंकि कुल पथ की लंबाई (AB + BC) विस्थापन (AC) से अधिक है, इसलिए कण की औसत चाल उसके औसत वेग से अधिक है। यदि कण सीधी रेखा में चलता है, तो किसी निश्चित अवधि में विस्थापन उसके द्वारा वास्तव में तय किए गए पथ के बराबर होता है। इस परिदृश्य में, औसत चाल औसत वेग के बराबर होती है।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए गति के उदाहरण में वस्तु को लगभग बिंदु वस्तु माना जा सकता है:
दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लंबा है और 1s समय लगता है। उसकी गति का x - t ग्राफ खींचिए। ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहाँ से चलना प्रारंभ करता है वहाँ से 13 m दूर किसी गड्ढे में कितने समय पश्चात गिरता है?
नीचे दिए गए कथन को ध्यान से पढिए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य:
एकविमीय गति में किसी कण की किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है।
चित्र में के ग्राफ को ध्यान से देखिए और देखकर बताइए कि वह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता।

नीचे दिए गए गति के उदाहरण में वस्तु को लगभग बिंदु वस्तु माना जा सकता है:
किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर।
नीचे दिए गए गति के उदाहरण में वस्तु को लगभग बिंदु वस्तु माना जा सकता है:
जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
नीचे दिए गए गति के उदाहरण में वस्तु को लगभग बिंदु वस्तु माना जा सकता है:
किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
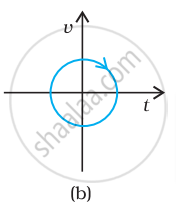
चित्र में के ग्राफ को ध्यान से देखिए और देखकर बताइए कि वह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता।
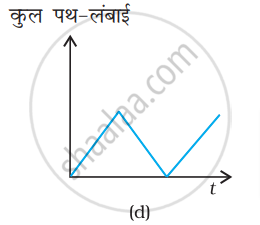
चित्र में के ग्राफ को ध्यान से देखिए और देखकर बताइए कि वह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता।
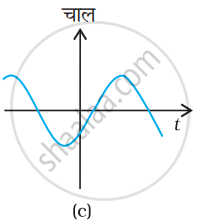
चित्र में के ग्राफ को ध्यान से देखिए और देखकर बताइए कि वह ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता।