Advertisements
Advertisements
प्रश्न
Using Ampere's Law, derive an expression for the magnetic induction inside an ideal solenoid carrying a steady current.
उत्तर
- Consider an ideal solenoid as shown in the figure below.
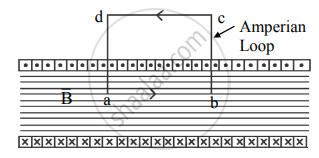
Ampere’s law applied to a part of a long ideal solenoid - The dots (.) show that the current is coming out of the plane of the paper and the crosses (×) show that the current is going into the plane of the paper, both in the coil of square cross-section wire.
- For the application of Ampere's law, an Amperian loop is drawn as shown in the figure and box.
- Using Ampere’s law,
`ointvec"B".vec"d""l" = mu_0"I"`
Over the rectangular loop abcd, the above integral takes the form
`int_"a"^"b" vec"B".vec"d""l" + int_"b"^"c" vec"B".vec"d""l" + int_"c"^"d" vec"B".vec"d""l" + int_"d"^"a" vec"B".vec"d""l" = mu_0"I"`
where, I is the net current encircled by the loop.
∴ BL + 0 + 0 + 0 = `mu_0"I"` ….(1)
Here, the second and fourth integrals are zero because `vec"B"` and `vec"d""l"` are perpendicular to each other. The third integral is zero because outside the solenoid, B = 0. - If the number of turns is n per unit length of the solenoid and the current flowing through the wire is i, then the net current coming out of the plane of the paper is
I = nLi
∴ Using equation (1)
BL = `mu_0"nLi"`
∴ B = `mu_0"ni"` ….(2)
Equation (2) is the required expression.
APPEARS IN
संबंधित प्रश्न
A solenoid of length π m and 5 cm in diameter has winding of 1000 turns and carries a current of 5 A. Calculate the magnetic field at its center along the axis.
What is Solenoid?
What is Toroid?
A solenoid of length 50 cm of the inner radius of 1 cm and is made up of 500 turns of copper wire for a current of 5 A in it. What will be the magnitude of the magnetic field inside the solenoid?
Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid Why?
A toroid of 4000 turns has an outer radius of 26 cm and an inner radius of 25 cm. If the current in the wire is 10 A. Calculate the magnetic field of the toroid.
The length of solenoid is I whose windings are made of material of density D and resistivity p. The winding resistance is R. The inductance of solenoid is
[m = mass of winding wire, µ0 = permeability of free space]
A winding wire which is used to frame a solenoid can bear a maximum of 20 A current. If the length of the solenoid is 80 cm and its cross-sectional radius is 3 cm, then the required length of winding wire is ______ (B = 0.2 T)
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 2,000 turns of a wire are wound. If the current in the wire is 10 A, the magnetic field inside the core of the toroid will be ______
Two current-carrying coils have radii r and 4r and have same magnetic induction at their centres. The ratio of voltage applied across them is ______.
Two toroids 1 and 2 have total number of turns 400 and 200 respectively with average radii 40 cm and 20 cm respectively. If they carry same current I, the ratio of the magnetic fields along the two loops is, ____________.
A 600 turn coil of effective area 0.05 m2 is kept perpendicular to a magnetic field 4 x 10-5 T. When the plane of the coil is rotated by 90° around any of its coplanar axis in 0.1 s, the e.m.f. induced in the coil will be: ____________.
The magnetic induction along the axis of a toroidal solenoid is independent of ______.
The space within a current carrying toroid is filled with a m metal of susceptibility 16.5 x 10-6. The percentage increase in the magnetic field B is ____________.
A toroid is a long coil of wire wound over a circular core. If 'r' and 'R' are the radii of the coil and toroid respectively, the coefficient of self-induction of the toroid is (The magnetic field in it is uniform and R > > r) ____________.
(N = number of turns of the coil and µ0 = permeability of free space)
A long solenoid carrying current 'I1' produces magnetic field 'B1' along its axis. If the current is reduced to 25% and number of turns per cm are increased four times, then new magnetic field 'B2' is ____________.
A winding wire is used to prepare a solenoid that can bear a maximum current of 10A. If the length of a solenoid is 80 cm and its cross-sectional radius is 3 cm, the required length of winding wire is ____________.
(magnetic field B = 0.2 T, µ0 = 4 x 10-7 SI units)
A charged particle carrying a charge 'q' and moving with velocity V, enters into a solenoid carrying a current T, along its axis. If 'B' is the magnetic induction along the axis of a solenoid, then the force 'F' acting on the charged particle will be ____________.
A toroid has a core of inner radius 20 cm and outer radius 22 cm around which 4200 turns of a wire are wound. If the current in the wire is 10 A. What is the magnetic field inside the core of toroid?
A long solenoid has 200 turns per cm and carries a current of 2.5 A. The magnetic field at the center is ______. (µ0 = 4π × 10-7 Wb/m-A)
A straight solenoid has 50 turns per cm in primary and 200 turns per cm in the secondary. The area of cross-section of the solenoid is 4 cm2. The mutual inductance is ______.
Obtain an expression for magnetic induction of a toroid of ‘N’ turns about an axis passing through its centre and perpendicular to its plane.
A conducting rod along the equator is 1 m long and carries a current of 15 A from east to west. The magnitude of Earth's magnetic field at the equator is `4/3 xx 10^(-4)` T. The magnitude and direction of the force on the rod are ______.
For a solenoid and a toroid, the number of turns per unit length is n and the respective interior volume is V. The self inductance is proportional to n2 and V for ______.
A current of 10 A passes through a coil having 5 turns and produces magnetic field at the centre of the coil having magnitude 0.5 x 10-4 T. Calculate diameter of the coil.
(µ0 = 4π x 10-7 Wb/Am)
