Advertisements
Advertisements
प्रश्न
Using Euler's formula find the unknown:
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
उत्तर
\[\text { We know that the Euler's formula is: F+V = E+2 }\]
1 .\[\text { The number of vertices V is 6 and the number of edges E is 12 }.\]
\[\text { Using Euler's formula: }\]
\[\text { F+6 = 12+2 }\]
\[\text { F+6 = 14 }\]
\[\text { F = 14-6 }\]
\[\text { F = 8 }\]
\[\text { So, the number of faces in this polyhedron is 8 }.\]
2. \[\text { Faces, F = 5 }\]
\[\text { Edges, E = 9}.\]
\[\text { We have to find the number of vertices }.\]
\[\text { Putting these values in Euler's formula: }\]
\[\text { 5+V = 9+2 }\]
\[\text { 5+V = 11 }\]
\[\text { V = 11-5 }\]
\[\text { V = 6 }\]
\[\text { So, the number of vertices in this polyhedron is 6 }.\]
3. \[\text { Number of faces F = 20 }\]
\[\text { Number of vertices V = 12 }\]
\[\text { Using Euler's formula: }\]
\[\text { 20+12 = E+2 }\]
\[\text { 32 = E+2 }\]
\[\text { E+2 = 32 }\]
\[\text { E = 32-2 }\]
\[\text { E = 30 }.\]
\[\text { So, the number of edges in this polyhedron is 30 }.\]
APPEARS IN
संबंधित प्रश्न
The given Figure are prisms or not?
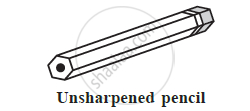
The given Figure are prisms or not?
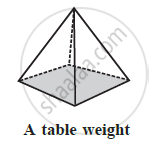
What is the least number of planes that can enclose a solid? What is the name of the solid?
Is it possible to have a polyhedron with any given number of faces?
Is a square prism same as a cube?
Verify Euler's formula for the following polyhedron:
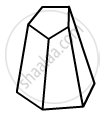
Verify Euler's formula for the following polyhedron:
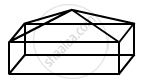
The dimensions of a cuboid are 6 cm, 4 cm and 3 cm. Draw two different types of oblique sketches for this cuboid.
Verify Euler’s formula for the table given below.
| Faces | Verticles | Edges |
| 12 | 20 | 30 |
The common portion of two adjacent faces of a cuboid is called ______.
