Advertisements
Advertisements
प्रश्न
Using Gauss's law in electrostatics, deduce an expression for electric field intensity due to a uniformly charged infinite plane sheet. If another identical sheet is placed parallel to it, show that there is no electric field in the region between the two sheets ?
उत्तर
Electric Field Due to a uniformly charged infinitely large plane thin sheet with surface charge density σ, using Gauss's law
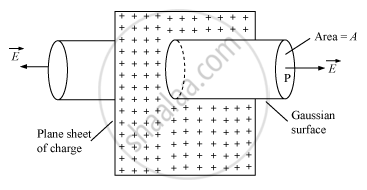
Consider an infinite thin plane sheet of positive charge with a uniform surface charge density σ on both sides of the sheet. Let P be the point at a distance a from the sheet at which the electric field is required. Draw a Gaussian cylinder of area of cross-section A through point P.
The electric flux crossing through the Gaussian surface,
Φ = E × Area of the circular caps of the cylinder
Since electric lines of force are parallel to the curved surface of the cylinder, the flux due to the electric field of the plane sheet of charge passes only through the two circular caps of the cylinder.
Φ = E × 2A … (1)
According to Gauss' Theorem,
`ø q/ε_0`
Here, the charge enclosed by the Gaussian surface,
q = σA
`ø = (σA)/c_0` ...... (2)
From equations (i) and (ii), we get:
`Exx 2A =(σA)/ε_0`
`E = σ/(2ε_0)`
Consider two infinite plane parallel sheets of charge A and B. Let σ1 and σ1 be the uniform surface charge on A and B respectively.
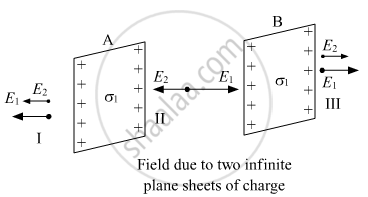
Therefore net electric field (E) between the two sheets can be found out as follows:
\[\text { Electric field due to sheet A }\]
\[ E_1 = \frac{\sigma_1}{2 \epsilon_o} \]
\[\text { Electric field due to sheet B }\]
\[ E_2 = \frac{\sigma_1}{2 \epsilon_o}\]
\[E = E_1 - E_2 \]
\[ = \frac{\sigma_1}{2 \epsilon_o} - \frac{\sigma_1}{2 \epsilon_o} = 0\]
Hence, there is no electric field in the region between the two sheets.
APPEARS IN
संबंधित प्रश्न
Find the electric field intensity due to a uniformly charged spherical shell at a point (i) outside the shell. Plot the graph of electric field with distance from the centre of the shell.
Find the electric field intensity due to a uniformly charged spherical shell at a point (ii) inside the shell. Plot the graph of electric field with distance from the centre of the shell.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10−22 C/m2. What is E:
- in the outer region of the first plate,
- in the outer region of the second plate, and
- between the plates?
Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same.
Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
A spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it, without altering the charge, will the field inside be changed? What happens if the shell is made of a metal?
A positive point charge Q is brought near an isolated metal cube.
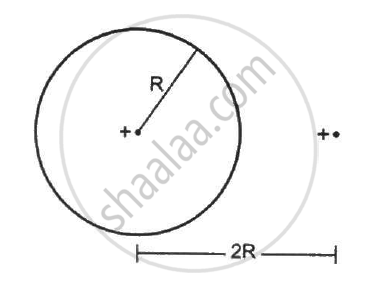
Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.
A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the centre due to the remaining wire.
