Question

Using ruler and compasses only, construct a parallelogram ABCD using the following data: AB = 6 cm, AD = 3 cm and ∠DAB = 45^o. If the bisector of ∠DAB meets DC at P,
prove that ∠APB is a right angle.

Answer 1

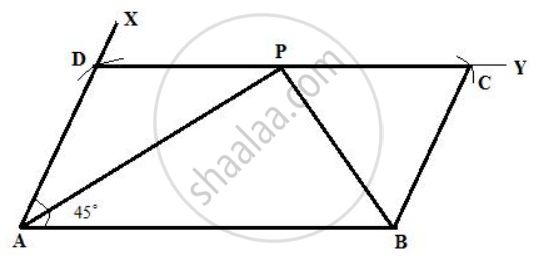
Steps:

1. draw AB = 6cm.

2. With A as a center draw a line AX such that ∠BAX = 45°.

3. With A as a center and radii, 3 cm draw an arc on AD.

4. now with D and B as a center and radii 6 cm and 3 cm draw arcs cutting each other at C.

5. Join DC and BC.

ABCD is the required parallelogram.
Here
∠PAB = ∠APD                ...[ Alternate angles ]
∠CPB = ∠PBA                 ...[ Alternate angles ] 

Now,
∠DPA + ∠APB + ∠CPB = 180° …… (i)

Also, considering APB,
∠PAB + ∠PBA + ∠APB = 180° …… (ii)

Therefore, from (i) and (ii)
∠APB = 90°
Hence proved.