Advertisements
Advertisements
प्रश्न
When proving that a quadrilateral is a trapezium, it is necessary to show
विकल्प
Two sides are parallel
Two parallel and two non-parallel sides
Opposite sides are parallel
All sides are of equal length
उत्तर
When proving that a quadrilateral is a trapezium, it is necessary to show Two parallel and two non-parallel sides
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If the area of the rectangle is three times the area of the square; find the dimensions of each.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
The perimeter of a rectangular field is `3/5`km. If the length of the field is twice its width; find the area of the rectangle in sq. meters.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Find the diagonal of a quadrilateral whose area is 756cm2 and the perpendicular from the opposite vertices are 17cm and 19cm.
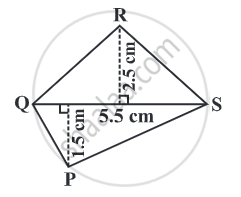
Find the area of quadrilateral PQRS.
PQRS is a rectangle formed by joining the points P(– 1, – 1), Q(– 1, 4), R(5, 4) and S(5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
