Advertisements
Advertisements
प्रश्न
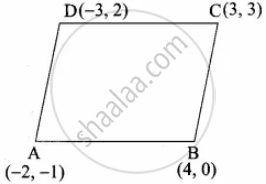
Without using distance formula, show that the points (−2, −1), (4, 0), (3, 3) and (−3, 2) are vertices of a parallelogram
उत्तर
The vertices A(−2, −1), B(4, 0), C(3, 3) and D(−3, 2)
Slope of a line = `(y_2 - y_1)/(x_2 - x_1)`
Slope of AB = `(0 + 1)/(4 + 2) = 1/6`
Slope of BC = `(3 - 0)/(3 - 4) = 3/(-1)` = −3
Slope of CD = `(2 - 3)/(-3 - 3) = (-1)/(-6) = 1/6`
Slope of AD = `(2 + 1)/(-3 + 2) = 3/(-1)` = −3
Slope of AB = Slope of CD = `1/6`
∴ AB || CD ...(1)
Slope of BC = Slope of AD = −3
∴ BC || AD ...(2)
From (1) and (2) we get ABCD is a parallelogram.
APPEARS IN
संबंधित प्रश्न
What is the slope of a line whose inclination with positive direction of x-axis is 90°
What is the slope of a line whose inclination with positive direction of x-axis is 0°
What is the inclination of a line whose slope is 0
What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (–6, 4).
Show that the given points are collinear: (– 3, – 4), (7, 2) and (12, 5)
Show that the given points form a right angled triangle and check whether they satisfy Pythagoras theorem
A(1, – 4), B(2, – 3) and C(4, – 7)
Show that the given points form a right angled triangle and check whether they satisfy Pythagoras theorem.
L(0, 5), M(9, 12) and N(3, 14)
Show that the given points form a parallelogram:
A(2.5, 3.5), B(10, – 4), C(2.5, – 2.5) and D(– 5, 5)
The slope of the line joining (12, 3), (4, a) is `1/8`. The value of ‘a’ is
If slope of the line PQ is `1/sqrt(3)` then slope of the perpendicular bisector of PQ is
