Advertisements
Advertisements
प्रश्न
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(30 < X < 35)
उत्तर
Given X ~ N(µ, σ2)
µ = 30
σ = 4
P(30 < X < 35) = ?
When x = 30
z = `(35 - 30)/4 = 5/4` = 1.25
P(30 < x < 35) = P(0 < z < 1.25)
= 0.3944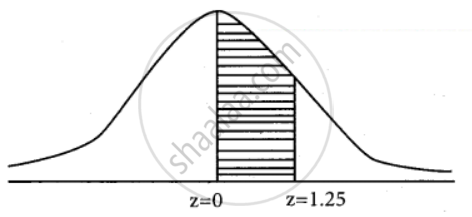
APPEARS IN
संबंधित प्रश्न
In a particular university 40% of the students are having newspaper reading habit. Nine university students are selected to find their views on reading habit. Find the probability that none of those selected have newspaper reading habit
The mean of a binomial distribution is 5 and standard deviation is 2. Determine the distribution
Write any 2 examples for Poisson distribution
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute three or more customers appear
Choose the correct alternative:
The parameters of the normal distribution f(x) = `(1/sqrt(72pi))"e"^(-(x - 10)^2)/72 - oo < x < oo`
Choose the correct alternative:
The average percentage of failure in a certain examination is 40. The probability that out of a group of 6 candidates atleast 4 passed in the examination are
Choose the correct alternative:
Monthly expenditure on their credit cards, by credit cardholders from a certain bank, follows a normal distribution with a mean of ₹ 1,295.00 and a standard deviation of ₹ 750.00. What proportion of credit cardholders spend more than ₹ 1,500.00 on their credit cards per month?
Choose the correct alternative:
Let z be a standard normal variable. If the area to the right of z is 0.8413, then the value of z must be:
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Less than 19.5 hours?
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time. Between 20 and 22 hours?
