Advertisements
Advertisements
प्रश्न
You are given three resistances of 1, 2 and 3 ohms. Shows by diagrams, how with the help of these resistances you can get:
(i) 6 Ω
(ii) `6/1` Ω
(iii) 1.5 Ω
उत्तर
To get a value of 6 Ω, all the resistors are to be connected in series as shown below:

Net resistance, R = R1 + R2 + R3
R = 1 Î + 2 Î + 3 Î = 6 Î
To get a value of 6 / 11 Ω, all the resistors are to be connected in parallel as shown below:
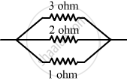
When tree resistance is conencted in parallel their resultant is given by
`1/R=1/R_1+1/R_2+1/R_3`
`R1=3 Ω
`R_2=2`Ω
`R_3=1` Ω
`1/R=1/3+1/2+1/1`
`1/R=(2+3+6)/6`
`1/R=11/6`
`R=6/11`Ω
To get a value of 1.5 Ω, the 1 Ω and 2 Ω resistors should be connected in series and this arrangement should be connected in parallel with the 3 Ω resistor as shown below:
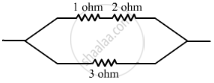
The resistors of resistance 1 Î and 2 Î are in series. Therefore, their net resistance is:
`R=R_1+R_2`
`R=1I+2I`
`R=3I`
This 3 Î is connected in parallel with another 3 Î resistance.
Therefore, net resistance will be:
`1/R=1/R_1+1/R_1`
`1/R=1/3+1/3`
`1/R=2/3`
`R=3/2=1.5`Ω
`1R=1R_1+1R_2 1R=13+131R=23R=32=1.5Ω`
APPEARS IN
संबंधित प्रश्न
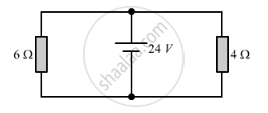
Find the current in each resistor in the circuit shown below:
An electric heater which is connected to a 220 V supply line has two resistance coils A and B of 24 Ω resistance each. These coils can be used separately (one at a time), in series or in parallel. Calculate the current drawn when:
(a) only one coil A is used.
(b) coils A and B are used in series.
(c) coils A and B are uses in parallel.
The figure given below shows three resistors?
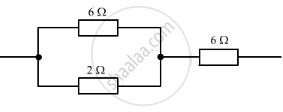
Their combined resistance is:
(a) `1 5/7`Ω
(b) `14` Ω
(c) `6 2/3` Ω
(d) `7 1/2` Ω
How will you connect three resistors of resistances 2 Ω, 3 Ω, and 6 Ω to obtain a total resistance of 4 Ω, and 1 Ω?
Two exactly similar electric lamps are arranged (i) in parallel, and (ii) in series. If the parallel and series combination of lamps are connected to 220 V supply line one by one, what will be the ratio of electric power consumed by them?
State how are the two resistors joined with a battery when equivalent resistance is less than either of the two resistances.
What is the equivalent resistance of 5 equal resistors, each of value 2`Omega` 1 when oonnected in (a) Series ( b) ParaIleI?
A battery of e.m.f. 15 V and internal resistance 2 `Omega` is connected to tvvo resistors of 4 ohm and 6 ohm joined.
(i) In series,
(ii) In para 1 lel. Find in each case the electrica I energy spent per minute in 6 ohm resistor.
Two resistors when connected in parallel give the resultant resistance of 2 ohms, but when connected in series the effective resistance becomes 9 ohms. Calculate the value of each resistance.
You are given four ammeters A, B, C and D having the least counts mentioned below:
(I) Ammeter A with least count 0.25 A
(II) Ammeter B with least count 0.5 A
(III) Ammeter C with least count 0.05 A
(IV) Ammeter D with least count 0.1 A
Which of the ammeters would you prefer for doing an experiment to determine the equivalent resistance of two resistances most accurately, when connected in parallel?
