Advertisements
Advertisements
प्रश्न
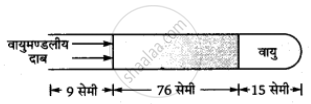
1 मीटर लंबी संकरी (और एक सिरे पर बंद) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए?
उत्तर
प्रारंभ में जब नली क्षैतिज है, तब बंद सिरे पर रोकी गई वायु का दाब वायुमंडलीय दाब के बराबर होगा क्योंकि यह वायु, वायुमंडलीय दाब के विरुद्ध पारे के स्तंभ को पीछे हटने से रोकती है।
∴ P1 = वायुमंडलीय दाब
= 76 cm पारद स्तंभ का दाब
यदि नली का अनुप्रस्थ क्षेत्रफल A cm² है तो वायु का आयतन V1 = 15 cm × A cm² = 15 A cm3। जब नली का खुला सिरा नीचे की ओर रखते हुए ऊर्ध्वाधर करते हैं तो खुले सिरे पर बाहर की ओर से वायुमंडलीय दाब (76 cm पारद स्तंभ का दाब) काम करता है जब कि ऊपर की ओर से 76 cm पारद सूत्र का दाब तथा बंद सिरे पर एकत्र वायु की दाब काम करते हैं। चूँकि खुले सिरे पर पारद स्तंभ + वायु का दाब अधिक है अतः पारद स्तंभ संतुलन में नहीं रह पाता और नीचे गिरते हुए, वायु को बाहर निकाल देता है।
माना पारद स्तंभ की h लंबाई नली से बाहर निकल जाती है।
तब, पारद स्तंभ की शेष ऊँचाई = (76 – h) cm
जबकि बंद सिरे पर वायु स्तंभ की लंबाई = (15 + 9 + h) cm
= (24 + h) cm
वायु का आयतन V2 = (24 + h) A cm3
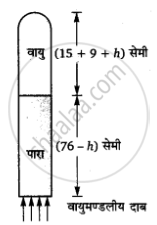
माना अब इस वायु का दाब P2 है तो संतुलन की स्थिति में
P2 + (76 + h) cm पारद स्तंभ का दाब = वायुमंडलीय दाब
= 76 cm पारद स्तंभ का दाब
अतः P2 = h cm पारद स्तंभ का दाब
P1V1 = P2V2 से, ...[∵ ताप नियत रहता है।]
76 cm × 15 A cm3 = h cm × (24 × h) cm3
या 1140 = 24h + h2
या h2 + 24h - 1140 = 0
`"h" = [(-24 ± sqrt((24)^2 - 4 xx 1 xx (-1140)))/(2 xx 1)]` cm
`= ((-24 ± 71.67)/2)` cm
अतः h = 23.8 cm अथवा – 47.8 cm (जो अनुमान्य है।)
इसलिए h = 23.8 cm ≈ 24 cm ।
अतः लगभग 24 सेमी पारा बाहर निकल जायेगा। शेष पारे का 52 सेमी ऊँचा स्तंभ तथा 4.8 सेमी वायु स्तंभ इसमें जुड़कर बाह्य वायुमंडल के साथ संतुलन में रहते हैं। (यहाँ पूरे प्रयोग की अवधि में ताप को नियत माना गया है तब ही बॉयल के नियम का प्रयोग किया है।)
APPEARS IN
संबंधित प्रश्न
नाइट्रोजन गैस के एक सिलिंडर में, 2.0 atm दाब एवं 17°C ताप पर, नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 Å लीजिए। संघट्ट-काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतंत्रतापूर्वक चलने में लगे समय से कीजिए। (नाइट्रोजन का आण्विक द्रव्यमान = 28.0u)
साम्यावस्था में किसी गैस का घनत्व और दाब अपने संपूर्ण आयतन में एकसमान हैं। यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो। उदाहरण के लिए गुरुत्व से प्रभावित किसी गैस स्तंभ का घनत्व (और दाब) एकसमान नहीं होता है। जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है। परिशुद्ध निर्भरता ‘वातावरण के नियम' `"n"_2 = "n"_1"exp"[- ("mg")/("k"_"B""T")("h"_2 - "h"_1)]` से दी जाती है, यहाँ n2, n1 क्रमशः h2 व h1 ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं। इस संबंध का उपयोग द्रव-स्तंभ में निलम्बित किसी कण के अवसादने साम्य के लिए समीकरण `"n"_2 = "n"_1"exp"[- ("m"_"g""N"_"A")/(rho "RT")(rho - rho^"'")("h"_2 - "h"_1)]` को व्युत्पन्न करने के लिए कीजिए, यहाँ ρ निलंबित कण का घनत्व तथा ρ’ चारों तरफ के माध्यम का घनत्व है। NA आवोगाद्रो संख्या तथा R सार्वत्रिक गैस नियतांक है। [संकेतः निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए ।]
नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं। उनके परमाणुओं की आमापों का आकलन (लगभग) कीजिए।
| पदार्थ | परमाणु द्रव्यमान (u) | घनत्व (103 kg m-3) |
| कार्बन (हिरा) | 12.01 | 2.22 |
| गोल्ड | 197.00 | 19.32 |
| नाइट्रोजन (द्रव) | 14.01 | 1.00 |
| लिथियम | 6.94 | 0.53 |
| फ्लुओरीन (द्रव) | 19.00 | 1.14 |
[ संकेतः मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में 'दृढ़ता से बँधे' हैं, तथा आवोगाद्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाणवीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिल्कुल अक्षरशः प्रयोग नहीं करना चाहिए क्योंकि दृढ़ संवेष्टन सन्निकटन की रूक्षता के परमाणवीय आकार कुछ Å के पास में हैं ]
